Условие:

11. Докажите, что у четырёхугольника, описанного около окружности, суммы длин противолежащих сторон равны.

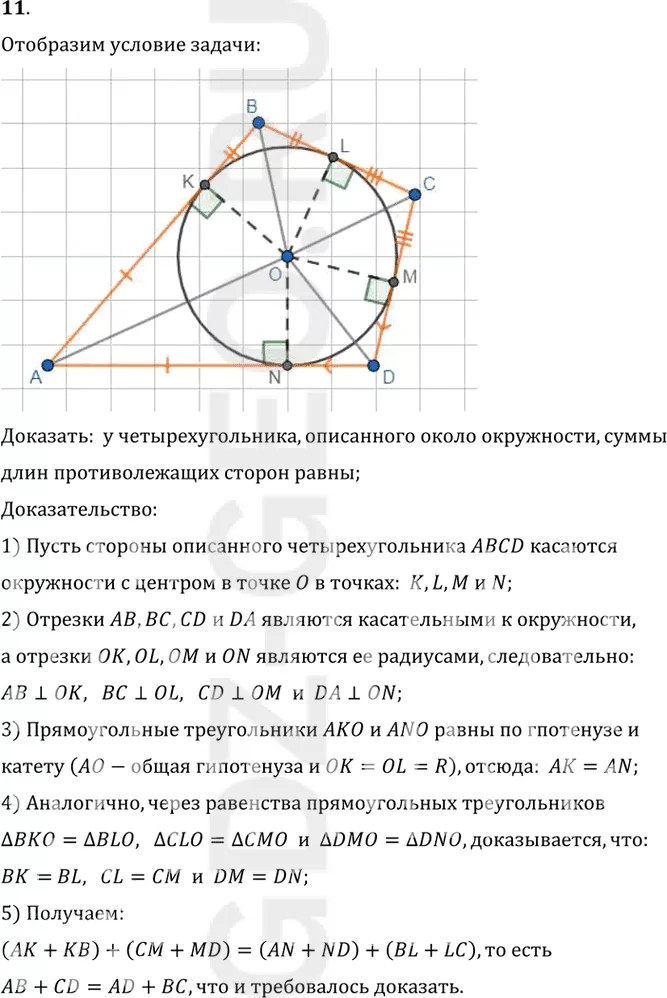
Доказать: у четырехугольника, описанного около окружности, суммы

длин противолежащих сторон равны;

Доказательство:

1) Пусть стороны описанного четырехугольника ABCD касаются

окружности с центром в точке O в точках: K, L, M и N;

2) Отрезки AB, BC, CD и DA являются касательными к окружности,

а отрезки OK, OL, OM и ON являются ее радиусами, следовательно:

AB?OK, BC?OL, CD?OM и DA?ON;

3) Прямоугольные треугольники AKO и ANO равны по гпотенузе и

катету (AO-общая гипотенуза и OK=OL=R), отсюда: AK=AN;

4) Аналогично, через равенства прямоугольных треугольников

треугольник BKO= треугольник BLO, треугольник CLO = треугольник CMO и треугольник DMO= треугольник DNO, доказывается, что:

BK=BL, CL=CM и DM=DN;

5) Получаем:

(AK+KB)+(CM+MD)=(AN+ND)+(BL+LC), то есть

AB+CD=AD+BC, что и требовалось доказать.

Развернуть