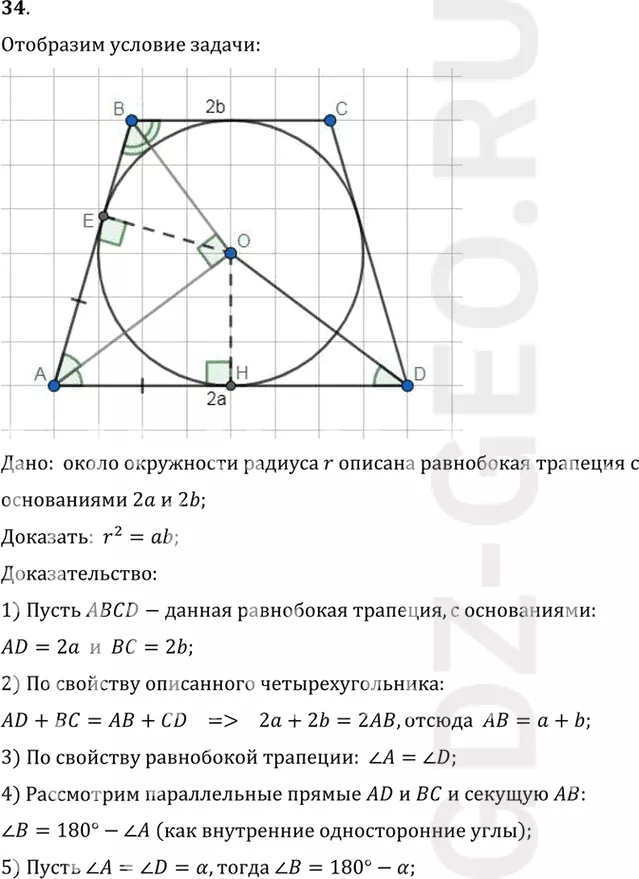
Условие:

34. Около окружности радиуса r описана равнобокая трапеция с основаниями 2а и 2b. Докажите, что r2 = ab.

Дано: около окружности радиуса r описана равнобокая трапеция с

основаниями 2a и 2b;

Доказать: r^2=ab;

Доказательство:

1) Пусть ABCD-данная равнобокая трапеция, с основаниями:

AD=2a и BC=2b;

2) По свойству описанного четырехугольника:

AD+BC=AB+CD => 2a+2b=2AB, отсюда AB=a+b;

3) По свойству равнобокой трапеции: угол A = углу D;

4) Рассмотрим параллельные прямые AD и BC и секущую AB:

угол B=180°- угол A (как внутренние односторонние углы);

5) Пусть угол A = углу D=альфа, тогда угол B=180°-альфа;

6) Отметим точку O-центр вписанной в трапецию ABCD окружности,

так как центр окружности равноудален от всех сторон описанного

четырехугольника, то точка O лежит на пересечении биссектрис данной

трапеции, тогда: угол ODA = углу OAD=1/2 угол A=альфа/2 и угол ABO=1/2 угол B=90°-альфа/2;

7) Опустим перпендикуляр OE на сторону AB и перпендикуляр OH на

сторону AD, тогда: OE=OH=r;

8) Прямоугольные треугольники OAH и ODH равны по катету и проти-

волежащему острому углу (OH-общий катет и угол ODH = углу OAH), отсюда:

AH=HD=AD/2=2a/2=a;

9) AE=AH=a (как отрезки касательных, проведенных из одной точки);

10) BE=AB-AE=a+b-a=b;

11) Рассмотрим треугольник BOA:

угол AOB=180°- угол BAO- угол ABO=180°-альфа/2-90°+альфа/2=90°;

12) В прямоугольном треугольнике BOA отрезок OE является высотой,

опущенной на гипотенузу, значит согласно доказанному в контрольном

вопросе 11 параграфа 11 он является средним пропорциональным между

проекциями катетов OA и OB на гипотенузу AB:

OE=v(AE•BE);

r=v(a•b) => r^2=ab, что и требовлось доказать.

Развернуть