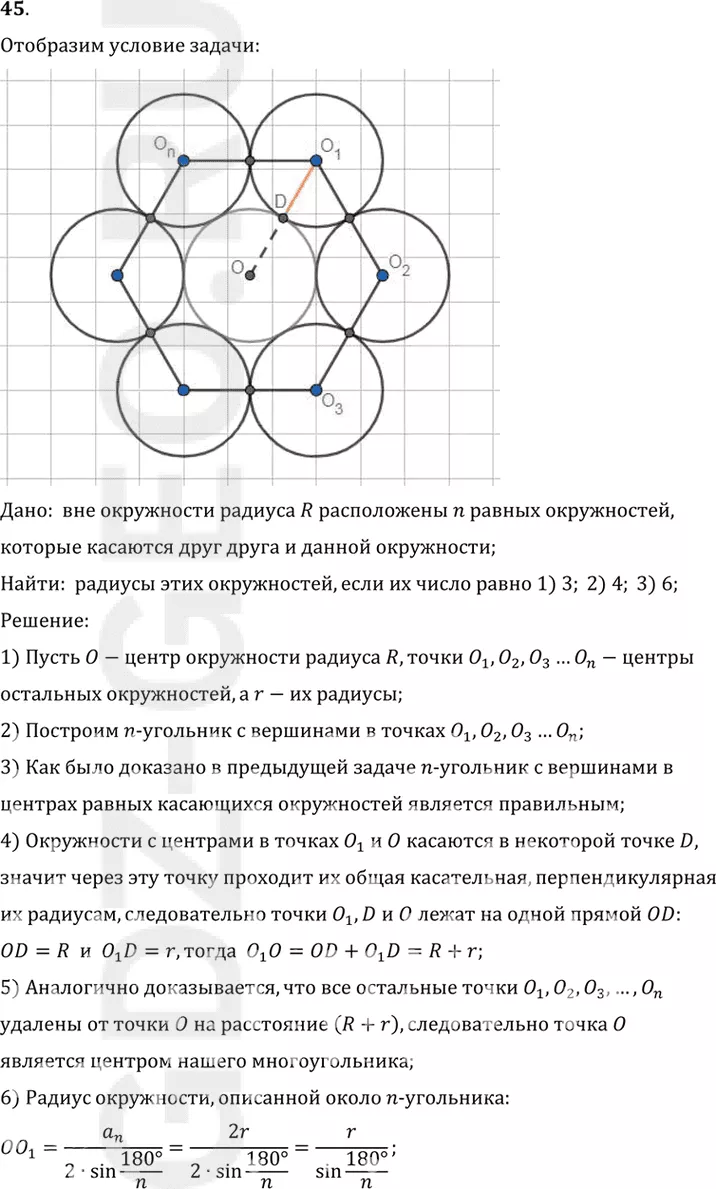
Условие:

45. Решите предыдущую задачу, если окружности расположены вне данной окружности.

Дано: вне окружности радиуса R расположены n равных окружностей,

которые касаются друг друга и данной окружности;

Найти: радиусы этих окружностей, если их число равно 1) 3; 2) 4; 3) 6;

Решение:

1) Пусть O-центр окружности радиуса R, точки O1, O2, O3…On-центры

остальных окружностей, а r-их радиусы;

2) Построим n-угольник с вершинами в точках O1, O2, O3…On;

3) Как было доказано в предыдущей задаче n-угольник с вершинами в

центрах равных касающихся окружностей является правильным;

4) Окружности с центрами в точках O1 и O касаются в некоторой точке D,

значит через эту точку проходит их общая касательная, перпендикулярная

их радиусам, следовательно точки O1, D и O лежат на одной прямой OD:

OD=R и O1 D=r, тогда O1 O=OD+O1 D=R+r;

5) Аналогично доказывается, что все остальные точки O1, O2, O3, …, On

удалены от точки O на расстояние (R+r), следовательно точка O

является центром нашего многоугольника;

6) Радиус окружности, описанной около n- угольника.

Развернуть