Условие:

15. Докажите, что правильные выпуклые д-угольники подобны. В частности, если у них стороны одинаковы, то они равны.

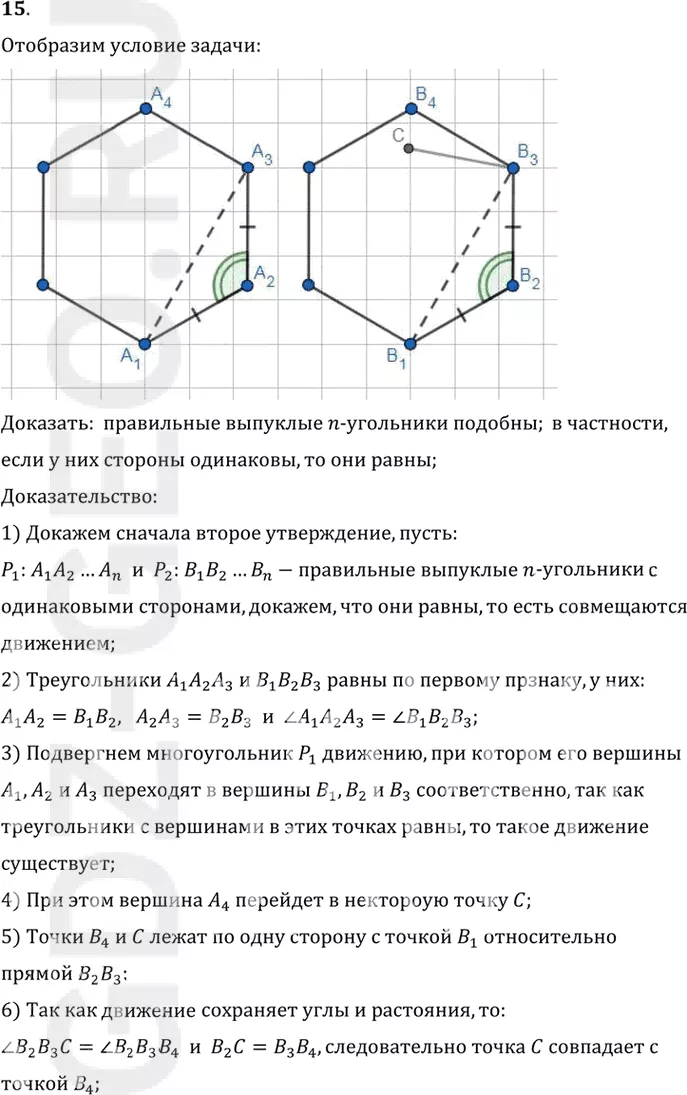
Доказать: правильные выпуклые n- угольники подобны; в частности,

если у них стороны одинаковы, то они равны;

Доказательство:

1) Докажем сначала второе утверждение, пусть:

P1: A1 A2…An и P2: B1 B2…Bn-правильные выпуклые n- угольники с

одинаковыми сторонами, докажем, что они равны, то есть совмещаются

движением;

2) Треугольники A1 A2 A3 и B1 B2 B3 равны по первому прзнаку, у них:

A1 A2=B1 B2, A2 A3=B2 B3 и угол A1 A2 A3 = углуB1 B2 B3;

3) Подвергнем многоугольник P1 движению, при котором его вершины

A1, A2 и A3 переходят в вершины B1, B2 и B3 соответственно, так как

треугольники с вершинами в этих точках равны, то такое движение

существует;

4) При этом вершина A4 перейдет в нектороую точку C;

5) Точки B4 и C лежат по одну сторону с точкой B1 относительно

прямой B2 B3;

6) Так как движение сохраняет углы и растояния, то:

угол B2 B3 C = углу B2 B3 B4 и B2 C=B3 B4, следовательно точка C совпадает с

точкой B4;

7) Таким образом, при нашем движении вершина A4 переходит в

вершину B4;

8) Далее таким же способом заключаем, что вершина A5 переходит в

вершину B5 и так далее, то есть многоугольник P1 переводится

движением в многоугольник P2, а значит они равны.

9) Теперь докажем первое утверждение, подвергнем сначала мноуголь-

ник P1 преобразованию подобия, наприсер гомотетии, с коэффициентом:

k=(B1 B2)/(A1 A2);

10) При этом получим правильный n- угольник P' с таким же сторонами,

как и у многоугольника P2;

11) По доказанному многоугольники P' и P2 равны, а так как n-угольники

P' и P1 подобны, то и треугольники P1 и P2 подобны, что и требоваось

Доказать.

Развернуть