Условие:

14. Сформулируйте и докажите свойство и признак описанного четырёхугольника.

I) Свойство и признак описанного четырехугольника:

В описанном четырехугольнике суммы противолежащих сторон равны;

и наоборот: если в выпуклом четырехугольнике суммы противолежащих

сторон равны, то в него можно вписать окружность;

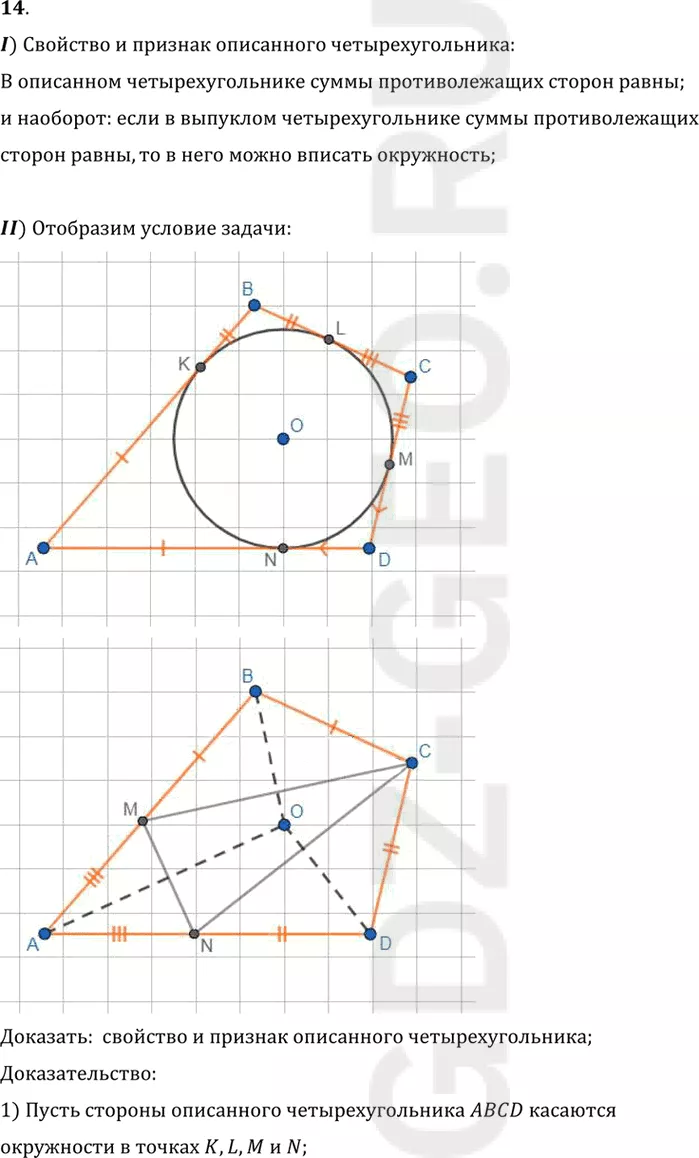
II) Отобразим условие задачи:

Доказать: свойство и признак описанного четырехугольника;

Доказательство:

1) Пусть стороны описанного четырехугольника ABCD касаются

окружности в точках K, L, M и N;

2) По свойству касательных, проведенных к окружности из одной точки:

AK=AN, BK=BL, CL=CM и DM=DN;

3) Получаем: (AK+KB)+(CM+MD)=(AN+ND)+(BL+LC), то есть

AB+CD=AD+BC, значит свойство описанного четырехугольника

доказано.

4) Обратно: пусть у выпуклого четырехугольника ABCD суммы

противолежащих сторон равны: AB+CD=BC+AD;

5) Если ABCD-ромб, то он является описанным около окружности с

центром в точке пересечения его диагоналей;

6) Рассмотрим теперь случай, когда у выпуклого четырехугольника

есть неравные соседние стороны;

7) Допустим, что AB>BC, а значит, AD>CD;

8) Отложим на сторонах с общей вершиной A следующие отрезки:

BM=BC, DN=CD;

9) AB+CD=BC+AD, отсюда AB-BC=AD-CD, значит:

AM=AB-BC=AD-CD=AN;

10) Треугольник AMN-равнобедренный с основанием MN;

11) Треугольник CBM-равнобедренный с основанием CM;

12) Треугольник CDN-равнобедренный с основанием CN;

13) По свойству медианы равнобедренного треугольника медианы этих

треугольников, проведенные к их основаниям, являются их высотами,

значит прямые, содержащие эти высоты-серединные перпендикуляры

к сторонам треугольника CMN и поэтому пересекаются в одной точке O;

14) Те же самые медианы являются и биссектрисами равнобедренных

треугольников AMN, CBM и CDN, поэтому лучи AO, BO и DO-биссектрисы

углов A, B и D четырехугольника ABCD, которые образуют с его сторонами

острые углы, так как по услвию данный четыреухгольник выпуклый;

15) Значит по свойсту биссектрисы точка O равноудалена от всех сторон

четырехугольника ABCD, и поэтому он является описанным около

окружности с центром в этой точке, следовательно признак описанного

четырехугольника доказан.

Развернуть