Условие:

13. Докажите, что площадь ромба равна половине произведения диагоналей.

Доказать: площадь ромба равна половине произведения диагоналей;

Доказательство:

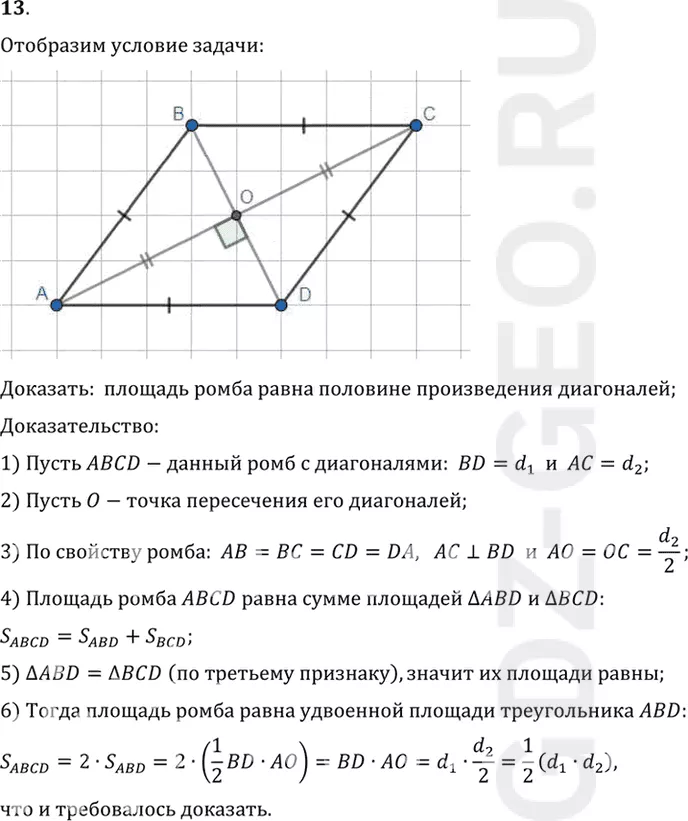
1) Пусть ABCD-данный ромб с диагоналями: BD=d1 и AC=d2;

2) Пусть O-точка пересечения его диагоналей;

3) По свойству ромба: AB=BC=CD=DA, AC перпендикулярен BD и AO=OC=d2/2;

4) Площадь ромба ABCD равна сумме площадей треугольника ABD и треугольника BCD:

SABCD=SABD+SBCD;

5) треугольник ABD = треугольник BCD (по третьему признаку), значит их площади равны;

6) Тогда площадь ромба равна удвоенной площади треугольника ABD:

SABCD=2•SABD=2•(1/2 BD•AO)=BD•AO=d1•d2/2=1/2 (d1•d2 ),

что и требовалось доказать.

Развернуть