Условие:

15. Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.

Разделить: данный треугольник на три равновеликие части прямыми,

проходящими через одну вершину;

Решение:

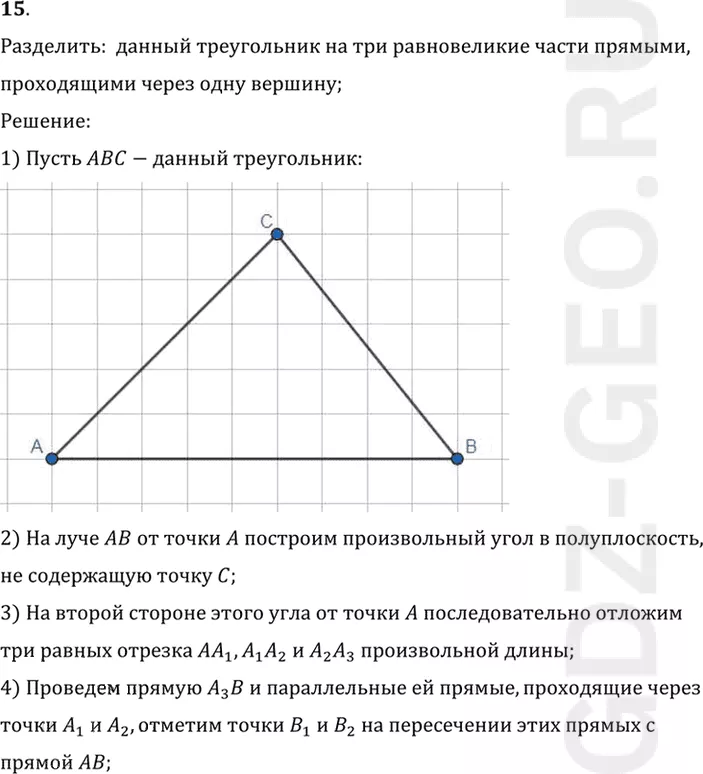
1) Пусть ABC-данный треугольник.

2) На луче AB от точки A построим произвольный угол в полуплоскость,

не содержащую точку C;

3) На второй стороне этого угла от точки A последовательно отложим

три равных отрезка AA1, A1 A2 и A2 A3 произвольной длины;

4) Проведем прямую A3 B и параллельные ей прямые, проходящие через

точки A1 и A2, отметим точки B1 и B2 на пересечении этих прямых с

прямой AB;

5) По теореме о пропорциональных отрезках: AB1=B1 B2=B2 B;

6) Треугольники ACB1, B1 CB2 и B2 CB имеют общую высоту, опущенную

из вершины C на прямую AB, следовательно их площади равны:

S(ACB1 )=S(B1 CB2 )=S(B2 CB)=1/2•1/3 AB•CH=1/3 SABC;

7) Прямые CB1 и CB2-искомые

Развернуть