Условие:

40. Докажите, что если диагонали четырёхугольника пересекаются, то площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

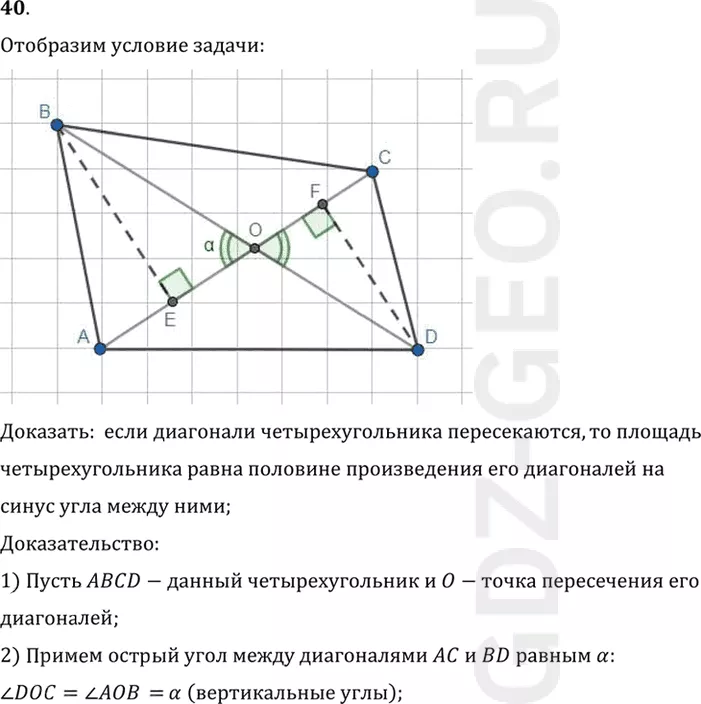
Доказать: если диагонали четырехугольника пересекаются, то площадь

четырехугольника равна половине произведения его диагоналей на

синус угла между ними;

Доказательство:

1) Пусть ABCD-данный четырехугольник и O-точка пересечения его

диагоналей;

2) Примем острый угол между диагоналями AC и BD равным альфа:

угол DOC=угол AOB=альфа (вертикальные углы);

3) На сторону AC опустим высоту BE треугольника ABC;

4) Рассмотрим прямоугольный треугольник BOE:

sin?угол AOB=BE/OB, отсюда BE=OB•sin угла AOB= BO•sinальфа;

5) На сторону AC опустим высоту DF треугольника ADC;

6) Рассмотрим прямоугольный треугольник DOF:

sin?угол DOC=DF/OD, отсюда DF=OD•sin угла DOC=OD•sin?альфа;

7) Площадь данного четырехугольника ABCD равна сумме площадей

треугольников ABC и ADC: S=SABC+SADC;

S=1/2 AC•BE+1/2 AC•DF=1/2 AC•BO•sinальфа+1/2 AC•DO•sinальфа=

=1/2 AC•(BO+OD)•sinальфа=1/2 AC•BD•sinальфа,

Что и требовалось доказать.

Развернуть