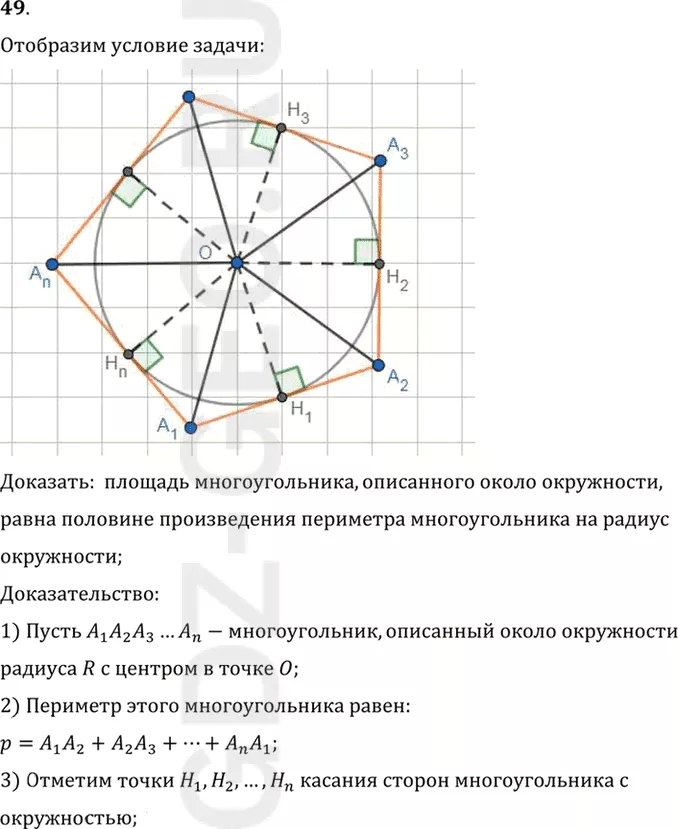
Условие:

49. Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.

Доказать: площадь многоугольника, описанного около окружности,

равна половине произведения периметра многоугольника на радиус

окружности;

Доказательство:

1) Пусть A1 A2 A3…An-многоугольник, описанный около окружности

радиуса R с центром в точке O;

2) Периметр этого многоугольника равен:

p=A1 A2+A2 A3+...+An A1;

3) Отметим точки H1, H2, …, Hn касания сторон многоугольника с

окружностью;

4) Отрезки OH1, OH2, OH3, …, OHn являются радиусами окружности:

OH1=OH2=...=OHn=R;

5) А так же по свойству касательной и радиуса они перпендикулярны

сторонам многоугольника;

6) Многоугольник A1 A2 A3…An состоит из треугольников:

A1 OA2, A2 OA3, …, An OA1 образованных его сторонами и отрезками

соединяющими его вершины с точкой O, а отрезки OH1, OH2, …, OHn

являются высотами этих треугольников;

5) Следовательно, площадь данного многоугольника равна:

S=S(A1 OA2)+S(A2 OA3 )+...+S(An OA1 );

S=1/2 A1 A2•OH1+1/2 A2 A3•OH2+...+1/2 An A1•OHn;

S=1/2 R•(A1 A2+A2 A3+...+An A1 )=p/2 R, что и требовалось доказать.

Развернуть