Условие:

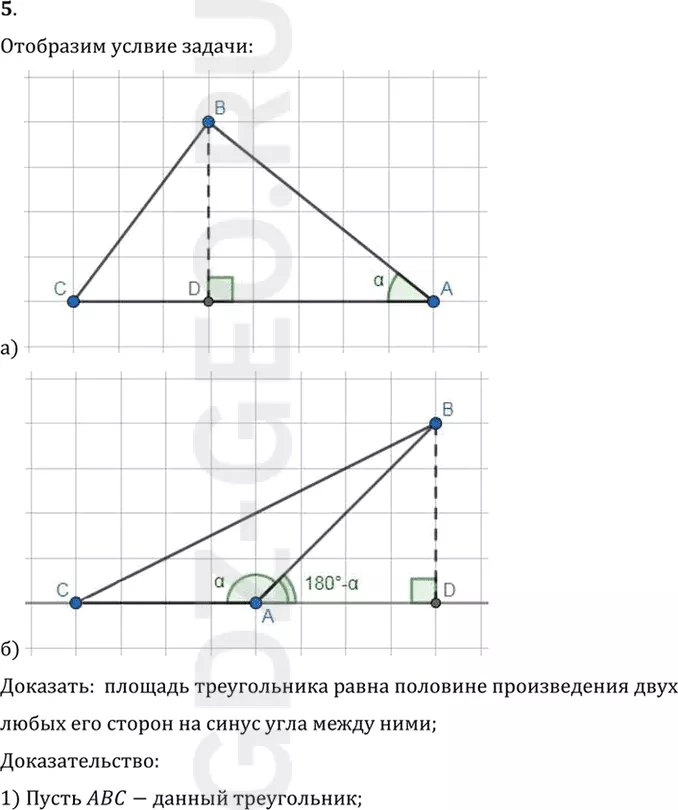
5. Докажите, что площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними.

Доказать: площадь треугольника равна половине произведения двух

любых его сторон на синус угла между ними;

Доказательство:

1) Пусть ABC-данный треугольник;

2) Из вершины B проведем высоту BD треугольника к стороне AC;

3) По доказанному в предыдущей задаче: S=1/2 AC•BD;

4) В прямоугольном треугольнике ABD:

- BD=AB•sin угла A, если угол A-острый (рисунок а);

- BD=AB•sin(180°-угол A), если угол A-тупой (рисунок б);

5) sin(180°-угол A)=sin угла A, следовательно в любом случае имеем:

BD=AB•sin угла A;

6) Значит площадь треугольника ABC равна:

S=1/2 AC•BD=1/2 AC•AB•sin угла A, что и требовалось доказать.

Развернуть