Условие:

6. Докажите, что площадь трапеции равна произведению полусуммы оснований на высоту.

Доказать: площадь трапеции равна произведению полусуммы

оснований на высоту;

Доказательство:

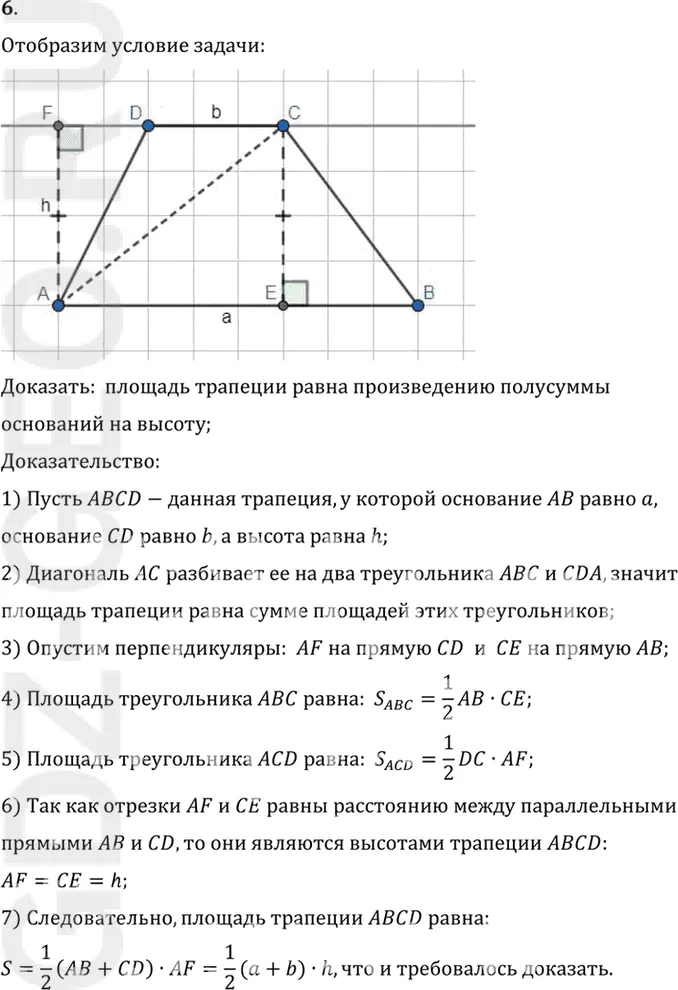
1) Пусть ABCD-данная трапеция, у которой основание AB равно a,

основание CD равно b, а высота равна h;

2) Диагональ AC разбивает ее на два треугольника ABC и CDA, значит

площадь трапеции равна сумме площадей этих треугольников;

3) Опустим перпендикуляры: AF на прямую CD и CE на прямую AB;

4) Площадь треугольника ABC равна: SABC=1/2 AB•CE;

5) Площадь треугольника ACD равна: SACD=1/2 DC•AF;

6) Так как отрезки AF и CE равны расстоянию между параллельными

прямыми AB и CD, то они являются высотами трапеции ABCD:

AF=CE=h;

7) Следовательно, площадь трапеции ABCD равна:

S=1/2 (AB+CD)•AF=1/2(a+b)•h, что и требовалось доказать.

Развернуть