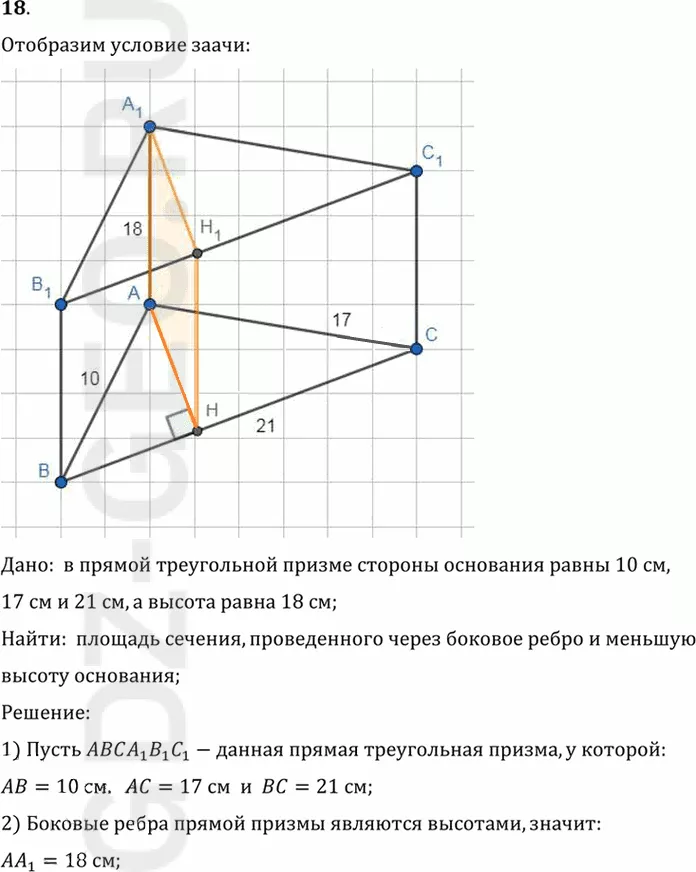
Условие:

18. В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см. Найдите площадь сечения, проведённого через боковое ребро и меньшую высоту основания.

Дано: в прямой треугольной призме стороны основания равны 10 см,

17 см и 21 см, а высота равна 18 см;

Найти: площадь сечения, проведенного через боковое ребро и меньшую

высоту основания;

Решение:

1) Пусть ABCA1 B1 C1-данная прямая треугольная призма, у которой:

AB=10 см, AC=17 см и BC=21 см;

2) Боковые ребра прямой призмы являются высотами, значит:

AA1=18 см;

3) Найдем площадь треугольника ABC по формуле Герона:

p=(10+17+21)/2=48/2=24 см;

SABC=v(24•(24-10)•(24-17)•(24-21) )=v(24•14•7•3)=

=v(8•3•7•2•7•3)=3•7•v(8•2)=21v16=21•4=84 см^2;

4) В треугольнике ABC сторона BC наибольшая, значит наименьшая

высота проведена к этой стороне, опустим эту высоту AH, тогда:

SABC=1/2•BC•AH, отсюда AH=(2SABC)/BC=(2•84)/21=8 см;

5) Из точки H опустим перпендикуляр HH1 на ребро B1 C;

6) Прямая AA1 перпендикулярна плоскости A1 B1 C1,значит она перпен-

дикулярна и отрезку B1 C1,лежащему в этой плоскости;

7) AA1?B1 C1 и HH1 перпендикулярен B1 C1,следовательно HH1||AA1;

8) Через прямые HH1 и AA1 можно провести плоскость, она пересечет

параллельные основания призмы по прямым AH и A1 H1,значит:

AH?A1 H1;

9) Таким образом, параллелограмм AA1 H1 H-искомое сечение:

уголAHH1=уголHH1 A1=90°, значит AA1 H1 H-прямоугольник;

10) Тогда площадь сечения равна:

S=AH•AA1=8•18=144 см^2;

Ответ: 144 см^2.

Развернуть