Условие:

21. По стороне основания а и боковому ребру b найдите полную поверхность правильной призмы: 1) треугольной; 2) четырёхугольной; 3) шестиугольной.

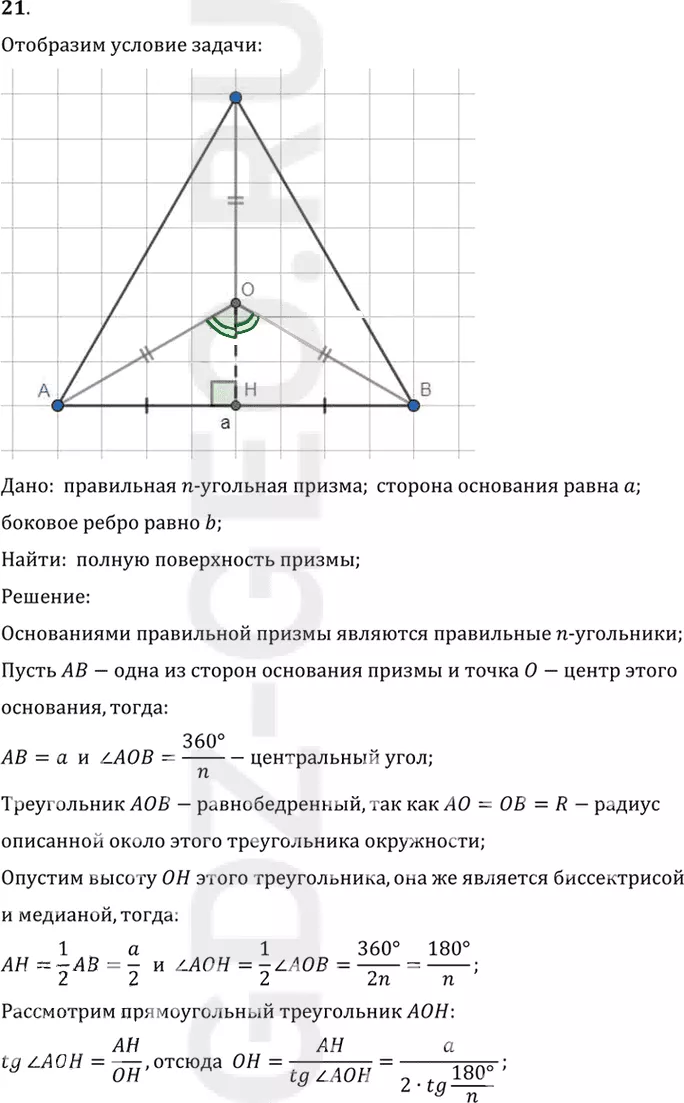
Дано: правильная n-угольная призма; сторона основания равна a;

боковое ребро равно b;

Найти: полную поверхность призмы;

Решение:

Основаниями правильной призмы являются правильные n-угольники;

Пусть AB-одна из сторон основания призмы и точка O-центр этого

основания, тогда:

AB=a и угол AOB=(360°)/n-центральный угол;

Треугольник AOB-равнобедренный, так как AO=OB=R-радиус

описанной около этого треугольника окружности;

Опустим высоту OH этого треугольника, она же является биссектрисой

и медианой, тогда:

AH=1/2 AB=a/2 и угол AOH=1/2угол AOB=(360°)/2n=(180°)/n;

Рассмотрим прямоугольный треугольник AOH:

tg угол AOH=AH/OH, отсюда OH=AH/(tg угол AOH)=a/(2•tg (180°)/n);

Каждое основание призмы состоит из n таких треугольников, равных треугольнику AOB, значит площадь оснований равна:

Sосн=2•n•SAOB=2n•1/2 AB•OH=an•a/(2•tg (180°)/n )=(na^2)/(2•tg (180°)/n);

Так как правильная призма является прямой, то ее боковая поверхность

состоит из n прямоугольников со сторонами a и b, значит ее площадь:

Sбок=n•ab;

Развернуть