Условие:

31. По данной стороне основания а и боковому ребру b найдите высоту правильной пирамиды: 1) треугольной; 2) четырёхугольной; 3) шестиугольной.

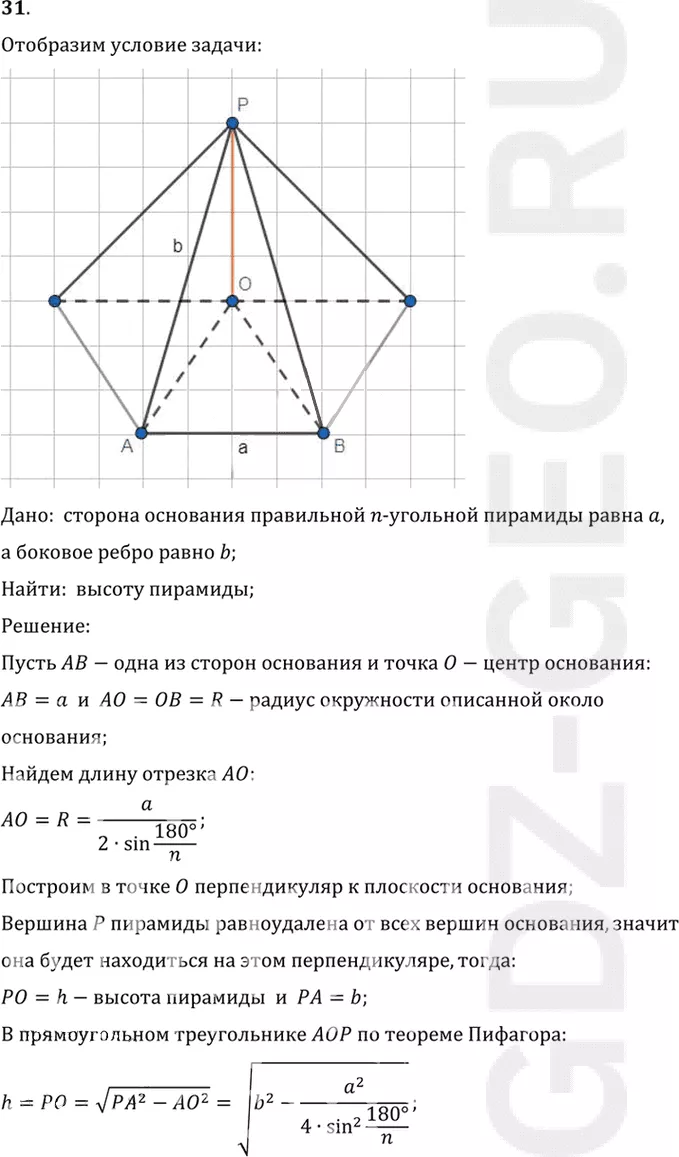
Дано: сторона основания правильной n-угольной пирамиды равна a,

а боковое ребро равно b;

Найти: высоту пирамиды;

Решение:

Пусть AB-одна из сторон основания и точка O-центр основания:

AB=a и AO=OB=R-радиус окружности описанной около

основания;

Найдем длину отрезка AO:

AO=R=a/(2•sin(180°)/n);

Построим в точке O перпендикуляр к плоскости основания;

Вершина P пирамиды равноудалена от всех вершин основания, значит

она будет находиться на этом перпендикуляре, тогда:

PO=h-высота пирамиды и PA=b;

В прямоугольном треугольнике AOP по теореме Пифагора:

h=PO=v(PA^2-AO^2)=v(b^2-a^2/(4•sin^2(180°)/n));

Развернуть