Условие:

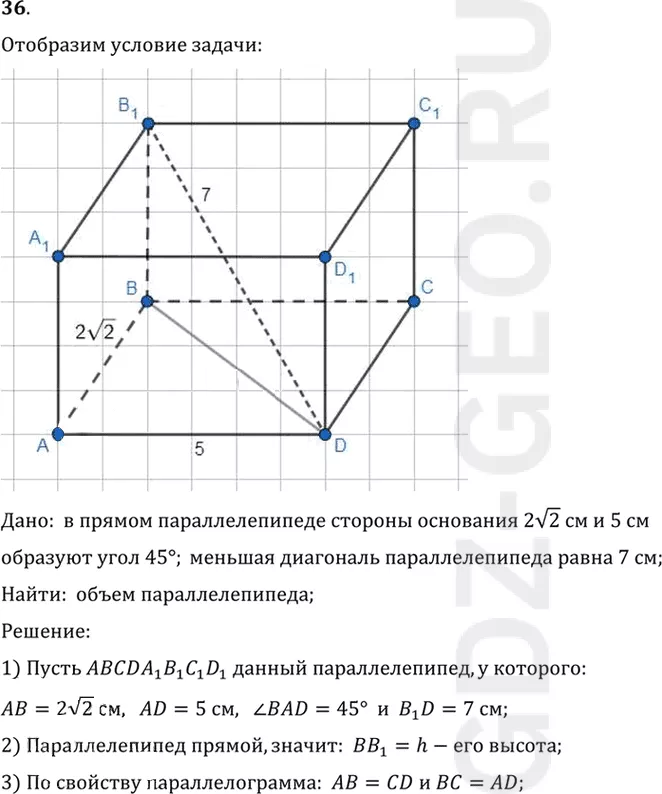
36. В прямом параллелепипеде стороны основания 2 корень 2 см и 5 см образуют угол 45°. Меньшая диагональ параллелепипеда равна 7 см. Найдите его объём.

Дано: в прямом параллелепипеде стороны основания 2v2 см и 5 см

образуют угол 45°; меньшая диагональ параллелепипеда равна 7 см;

Найти: объем параллелепипеда;

Решение:

1) Пусть ABCDA1 B1 C1 D1 данный параллелепипед, у которого:

AB=2v2 см, AD=5 см, угол BAD=45° и B1 D=7 см;

2) Параллелепипед прямой, значит: BB1=h-его высота;

3) По свойству параллелограмма: AB=CD и BC=AD;

4) Треугольники ABD и CBD равны по трем сторонам, значит площадь

параллелограмма ABCD равна:

Sосн=2•SABD=2•1/2•AB•AD•sinугол BAD;

Sосн=2v2•5•v2/2=2•5=10 см^2;

5) В треугольнике ABD по теореме косинусов:

BD^2=AB^2+AD^2-2AB•AD•cosугол BAD;

BD^2=4•2+25-2•2v2•5•cos45°;

BD^2=33-20v2•v2/2=33-20=13;

6) В прямоугольном треугольнике DBB1 по теореме Пифагора:

h=BB1=v(B1 D^2-BD^2 )=v(7^2-13)=v(49-13)=v36=6 см;

7) Найдем объем данного параллелепипеда:

V=Sосн•h=10•6=60 см^3;

Ответ: 60 см^3.

Развернуть