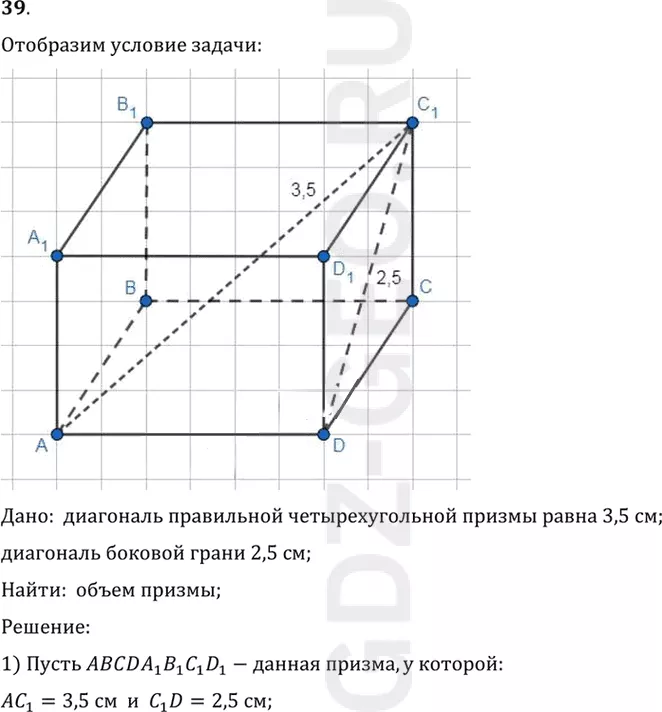
Условие:

39. Диагональ правильной четырёх угольной призмы равна 3,5 см, а диагональ боковой грани 2,5 см. Найдите объём призмы.

Дано: диагональ правильной четырехугольной призмы равна 3,5 см;

диагональ боковой грани 2,5 см;

Найти: объем призмы;

Решение:

1) Пусть ABCDA1 B1 C1 D1-данная призма, у которой:

AC1=3,5 см и C1 D=2,5 см;

2) Так как данная призма правильная, то ее основаниями являются

квадраты, а боковыми гранями-прямоугольники;

3) Проекция CD наклонной C1 D перпендикулярна прямой AD, значит

согласно теореме 15.3 наклонная C1 D также перпендикулярна AD;

4) В прямоугольном треугольнике ADC1 по теореме Пифагора:

AD=v(AC1^2-C1 D^2 )=v(3,5^2-2,5^2 )=v(12,25-6,25)=v6 см;

5) Так как ABCD-квадрат, то DC=AD=v6 см;

6) В прямоугольном треугольнике DCC1 по теореме Пифагора:

CC1=v(C1 D^2-DC^2 )=v(2,5^2-6)=v(6,25-6)=v0,25=0,5 см;

7) Найдем объем данной призмы:

S=Sосн•h=AD^2•CC1=6•0,5=3 см^3;

Ответ: 3 см^3.

Развернуть