Условие:

60. Равносторонний треугольник вращается вокруг своей стороны а. Найдите объём полученного тела вращения.

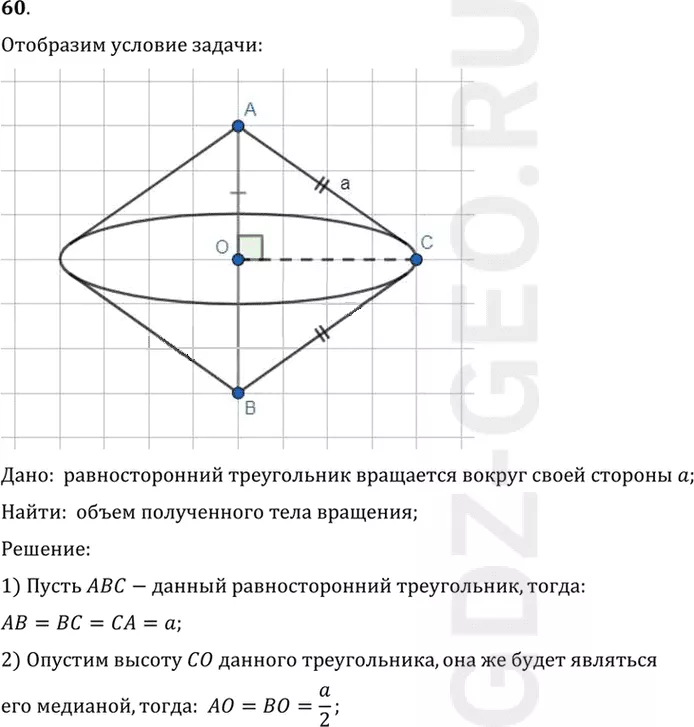
Дано: равносторонний треугольник вращается вокруг своей стороны a;

Найти: объем полученного тела вращения;

Решение:

1) Пусть ABC-данный равносторонний треугольник, тогда:

AB=BC=CA=a;

2) Опустим высоту CO данного треугольника, она же будет являться

его медианой, тогда: AO=BO=a/2;

3) В прямоугольном треугольнике AOC по теореме Пифагора:

OC^2=AC^2-AO^2=a^2-a^2/4=(3a^2)/4;

4) Рассмотрим тело F полученное вращением треугольника ABC вокруг

стороны AB, оно представляет собой два конуса с общим основанием,

радиусом которого является отрезок OC, и равными высотами AO и BO,

значит объемы этих двух конусов равны;

5) Следовательно, объем тела F равен удвоенному объему одного из этих

конусов:

V=2•1/3•Пи•OC^2•OA=2/3 Пи•(3a^2)/4•a/2=(Пиa^3)/4;

Ответ: (Пиa^3)/4.

Развернуть