Условие:
5.300. Найдите разность:
а) 13 8/9 - 4; б) 17 5/14 - 5 3/14; в) 9 5/7 - 3 6/7; г) 100 - 20 3/14.
Если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то, чтобы найти разность двух смешанных чисел, необходимо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
а) 13 8/9-4=(13-4)+8/9=9+8/9=9 8/9
б) 17 5/14-5 3/14=(17+5/14)-(5+3/14)=(17-5)+(5/14-3/14)=
=12+(5-3)/14=12+2/14=12 2/14
в) Если дробная часть уменьшаемого меньше дробной части вычитаемого, то сначала преобразовываем уменьшаемое так, чтобы дробь в нём получилась неправильная, для этого:
представляем уменьшаемое в виде суммы целой части и дробной части;
целую часть представляем в виде суммы единицы и числа, оставшегося от целой части после вычитания единицы;
единицу представляем в виде неправильной дроби, у которой числитель и знаменатель равны другу другу и равны знаменателю дробной части уменьшаемого;
полученную неправильную дробь складываем с дробной частью уменьшаемого;
складываем оставшуюся целую часть уменьшаемого с полученной неправильной дробью.
И затем выполняем вычитание.
9 5/7-3 6/7=(9+5/7)-(3+6/7)=(8+1+5/7)-(3+6/7)=
=(8+7/7+5/7)-(3+6/7)=(8+(7+5)/7)-(3+6/7)=
=(8+12/7)-(3+6/7)=(8-3)+(12/7-6/7)=5+(12-6)/7=5+6/7=
=5 6/7
г) Если уменьшаемое является целым числом и из него необходимо вычесть смешанное число или дробь, то преобразовываем это уменьшаемое так, чтобы в нём получилась неправильная дробь, для этого:
целое число представляем в виде суммы единицы и числа, оставшегося от него после вычитания единицы;
единицу представляем в виде неправильной дроби, у которой числитель и знаменатель равны другу другу и равны знаменателю дробной части вычитаемого;
складываем оставшееся целое число уменьшаемого с полученной неправильной дробью.
И затем выполняем вычитание.
100-20 3/14=(99+1)-20 3/14=(99+14/14)-(20+3/14)=
=(99-20)+(14/14-3/14)=79+(14-3)/14=79+11/14=79 11/14
Решение 1 - 5.3 - §5 Обыкновенные дроби:
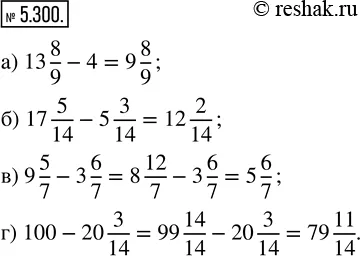
Решение 2 - 5.3:

Решение 3 - 5.3:

