Условие:
5.359. Выполните действие и сократите дробную часть полученного результата:
а) 14/18 - 5/18; б) 5/22 + 6/22; в) 6 7/12 - 1 3/12; г) 7 5/27 + 3 4/27.
При сложении смешанных чисел опираемся на правило, согласно которому, чтобы найти сумму двух смешанных чисел, необходимо отдельно сложить их целые и дробные части.
Если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то, чтобы найти разность двух смешанных чисел, необходимо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Согласно основному свойству дроби, если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
а) 14/18-5/18=(14-5)/18=9/18=(9•1)/(9•2)=1/2
б) 5/22+6/22=(5+6)/22=11/22=(11•1)/(11•2)=1/2
в) 6 7/12-1 3/12=(6+7/12)-(1+3/12)=(6-1)+(7/12-3/12)=
=5+(7-3)/12=5+4/12=5+(4•1)/(4•3)=5+1/3=5 1/3
г) 7 5/27+3 4/27=7+5/27+3+4/27=(7+3)+(5/27+4/27)=
=10+(5+4)/27=10+9/27=10+(9•1)/(9•3)=10+1/3=10 1/3
Решение 1 - 5.359 - §5 Обыкновенные дроби:
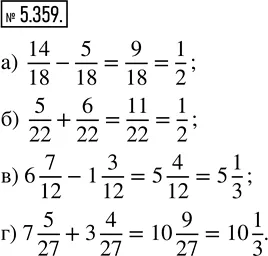
Решение 2 - 5.359:

