Условие:
5.379. Сократите дробь и выделите целую часть: а) 18/15; б) 21/14; в) 55/33; г) 168/40.
Согласно основному свойству дроби, если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
Если при сложении получается неправильная дробь, то выделяем из этой неправильной дроби целую часть.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, то есть выделить целую часть, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель дробной части.
а) 18/15=(3•6)/(3•5)=6/5=1 1/5
При выделении целой части из неправильной дроби 6/5 используем то, что 6:5=1 (ост.1).
б) 21/14=(7•3)/(7•2)=3/2=1 1/2
При выделении целой части из неправильной дроби 3/2 используем то, что 3:2=1 (ост.1).
в) 55/33=(11•5)/(11•3)=5/3=1 2/3
При выделении целой части из неправильной дроби 5/3 используем то, что 5:3=1 (ост.2).
г) 168/40=(4•42)/(4•10)=(2•21)/(2•5)=4 1/5
При выделении целой части из неправильной дроби 21/5 используем то, что 21:5=4 (ост.1).
Решение 1 - 5.379 - §5 Обыкновенные дроби:
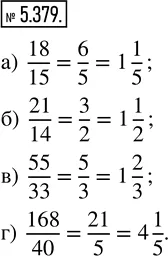
Решение 2 - 5.379:

Решение 3 - 5.379:

