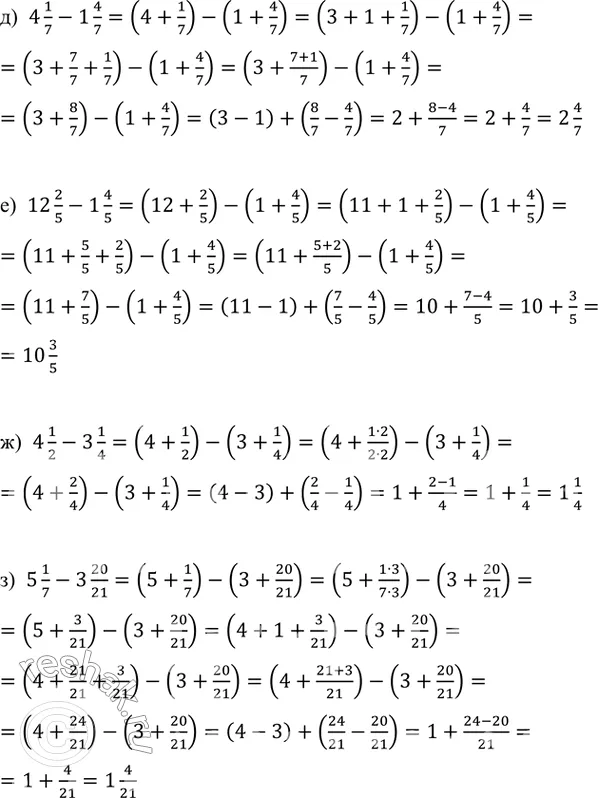Условие:
6.59. Найдите разность:
а) 7 3/5 - 1 2/5; в) 6 - 2/5; д) 4 1/7 - 1 4/7; ж) 4 1/2 - 3 1/4;
б) 28 6/13 - 7 1/13; г) 21 - 5/9; е) 12 2/5 - 1 4/5; з) 5 1/7 - 3 20/21.
Для того, чтобы найти разность двух смешанных чисел, необходимо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Для того, чтобы найти разность двух дробей с одинаковыми знаменателями, необходимо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Основное свойство дроби – если числитель и знаменатель дроби умножить на одно и то же число, то получится равная ей дробь.
а) 7 3/5-1 2/5=(7+3/5)-(1+2/5)=(7-1)+(3/5-2/5)=6+(3-2)/5=
=6+1/5=6 1/5
б) 28 6/13-7 1/13=(28+6/13)-(7+1/13)=(28-7)+(6/13-1/13)=
=21+(6-1)/13=21+5/13=21 5/13
в) 6-2/5=(5+1)-2/5=(5+5/5)-2/5=5+(5/5-2/5)=5+(5-2)/5=
=5+3/5=5 3/5
г) 21-5/9=(20+1)-5/9=(20+9/9)-5/9=20+(9/9-5/9)=
=20+(9-5)/9=20+4/9=20 4/9
д) 4 1/7-1 4/7=(4+1/7)-(1+4/7)=(3+1+1/7)-(1+4/7)=
=(3+7/7+1/7)-(1+4/7)=(3+(7+1)/7)-(1+4/7)=
=(3+8/7)-(1+4/7)=(3-1)+(8/7-4/7)=2+(8-4)/7=2+4/7=2 4/7
е) 12 2/5-1 4/5=(12+2/5)-(1+4/5)=(11+1+2/5)-(1+4/5)=
=(11+5/5+2/5)-(1+4/5)=(11+(5+2)/5)-(1+4/5)=
=(11+7/5)-(1+4/5)=(11-1)+(7/5-4/5)=10+(7-4)/5=10+3/5==10 3/5
ж) 4 1/2-3 1/4=(4+1/2)-(3+1/4)=(4+(1•2)/(2•2))-(3+1/4)=
=(4+2/4)-(3+1/4)=(4-3)+(2/4-1/4)=1+(2-1)/4=1+1/4=1 1/4
з) 5 1/7-3 20/21=(5+1/7)-(3+20/21)=(5+(1•3)/(7•3))-(3+20/21)=
=(5+3/21)-(3+20/21)=(4+1+3/21)-(3+20/21)=
=(4+21/21+3/21)-(3+20/21)=(4+(21+3)/21)-(3+20/21)=
=(4+24/21)-(3+20/21)=(4-3)+(24/21-20/21)=1+(24-20)/21=
=1+4/21=1 4/21
Решение 1 - 6.59 - §6 Десятичные дроби:
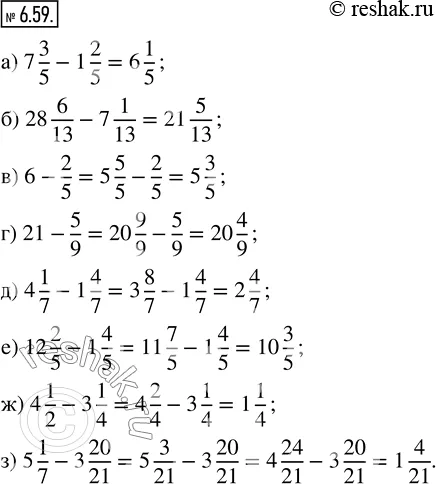
Решение 2 - 6.59:

Решение 3 - 6.59: