Условие:
6.188. Вместо знака вопроса поставьте одну и ту же цифру, чтобы было верно равенство или неравенство:
а) 4,?5 = 4,5?; 6) 2,?6 > 1,9?; в) 0,?7 < 0,4?; г) 0,2?9 < 0,37?.
При сравнении десятичных дробей опираемся на следующие правила:
- из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше;
- из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение).
а) 4,?5=4,5?
Таким образом, ?=5
б) 2,?6>1,9?
2,06>1,90
2,16>1,91
2,16>1,91
2,36>1,93
2,46>1,94
2,56>1,95
2,66>1,96
2,76>1,97
2,86>1,98
2,96>1,99
Таким образом, ? – любое число.
в) 0,?7<0,4?
0,17<0,41
0,27<0,42
0,37<0,43
0,47<0,44 – не верно.
Таким образом, ? = 0, 1, 2 или 3.
г) 0,2?9<0,37?
0,209<0,370
0,219<0,371
0,229<0,372
0,239<0,373
0,249<0,374
0,259<0,375
0,269<0,376
0,279<0,377
0,289<0,378
0,299<0,379
Таким образом, ? – любое число.
Решение 1 - 6.188 - §6 Десятичные дроби:
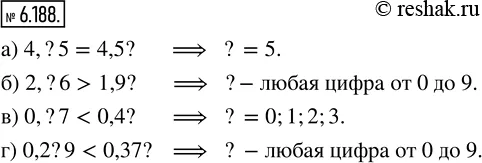
Решение 2 - 6.188:

Решение 3 - 6.188:

