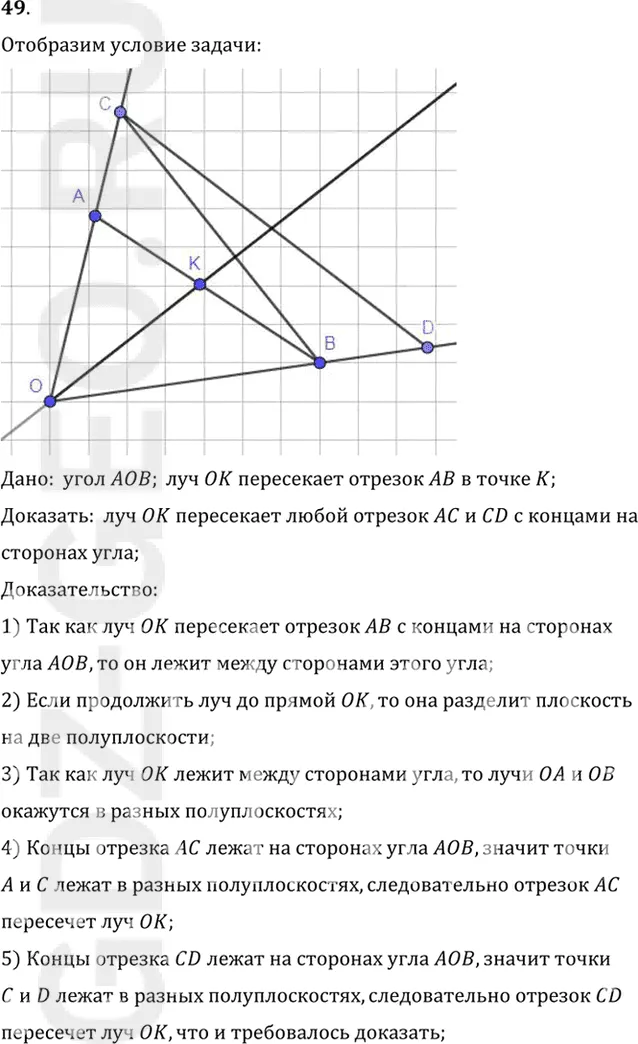
Условие:

49. Докажите, что если луч, исходящий из вершины угла, пересекает отрезок АВ с концами на сторонах угла, то он пересекает: 1) отрезок АС с концами на сторонах угла; 2) любой отрезок CD с концами на сторонах угла (рис. 30).

Дано: угол AOB; луч OK пересекает отрезок AB в точке K;

Доказать: луч OK пересекает любой отрезок AC и CD с концами на

сторонах угла;

Доказательство:

1) Так как луч OK пересекает отрезок AB с концами на сторонах

угла AOB, то он лежит между сторонами этого угла;

2) Если продолжить луч до прямой OK, то она разделит плоскость

на две полуплоскости;

3) Так как луч OK лежит между сторонами угла, то лучи OA и OB

окажутся в разных полуплоскостях;

4) Концы отрезка AC лежат на сторонах угла AOB, значит точки

A и C лежат в разных полуплоскостях, следовательно отрезок AC

пересечет луч OK;

5) Концы отрезка CD лежат на сторонах угла AOB, значит точки

C и D лежат в разных полуплоскостях, следовательно отрезок CD

пересечет луч OK, что и требовалось доказать;