Условие:

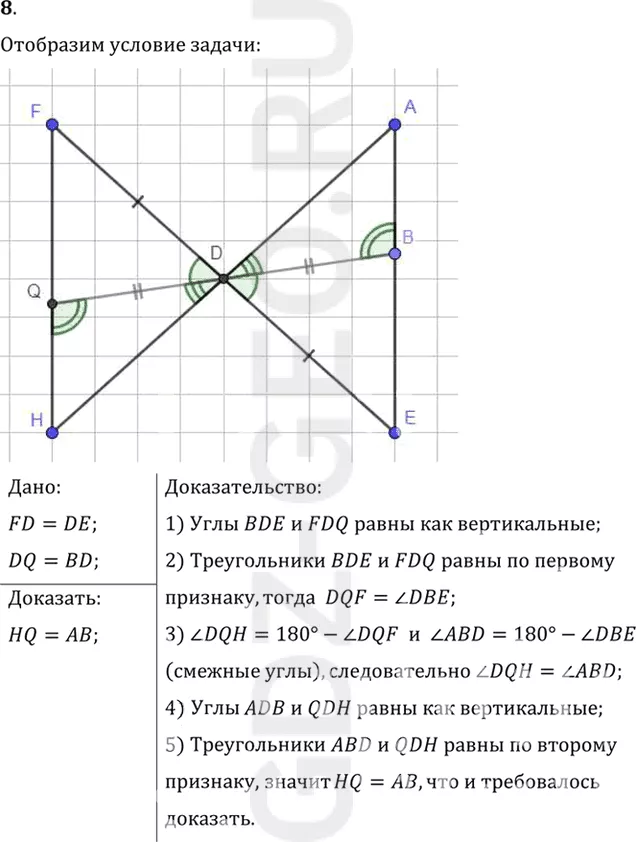
8. Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ (рис. 61) и на его продолжении отмеряют произвольный отрезок BE. Выбирают на местности точку D, из которой видна точка А и можно пройти к точкам В и Е. Провешивают прямые BDQ и EDF и отмеряют FD = DE и DQ = BD. Затем идут по прямой FQ, глядя на точку А, пока не найдут точку Н, которая лежит на прямой AD. Тогда HQ равно искомому расстоянию. Докажите.

Доказательство:

1) Углы BDE и FDQ равны как вертикальные;

2) Треугольники BDE и FDQ равны по первому

признаку, тогда DQF = углу DBE;

3) угол DQH=180°- угол DQF и угол ABD=180°- угол DBE

(смежные углы), следовательно угол DQH = углу ABD;

4) Углы ADB и QDH равны как вертикальные;

5) Треугольники ABD и QDH равны по второму

признаку, значит HQ=AB, что и требовалось

Доказать.