Условие:

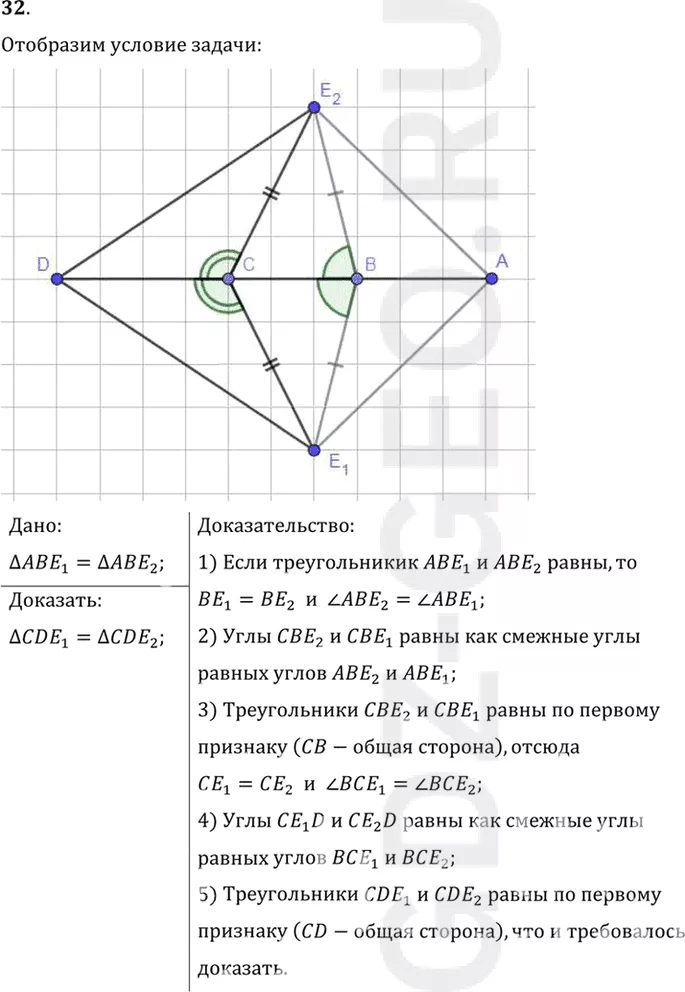
32. Точки А, В, С, В лежат на одной прямой. Докажите, что если треугольники АВЕ1 и АВЕ2 равны, то треугольники CDE1 и CDE2 тоже равны (рис. 65).

1) Если треугольникик ABE1 и ABE2 равны, то

BE1=BE2 и угол ABE2 = углу ABE1;

2) Углы CBE2 и CBE1 равны как смежные углы

равных углов ABE2 и ABE1;

3) Треугольники CBE2 и CBE1 равны по первому

признаку (CB-общая сторона), отсюда

CE1=CE2 и угол BCE1 = углу BCE2;

4) Углы CE1 D и CE2 D равны как смежные углы

равных углов BCE1 и BCE2;

5) Треугольники CDE1 и CDE2 равны по первому

признаку (CD-общая сторона), что и требовалось

Доказать.

Развернуть