Условие:

28. Докажите, что биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, является медианой и высотой.

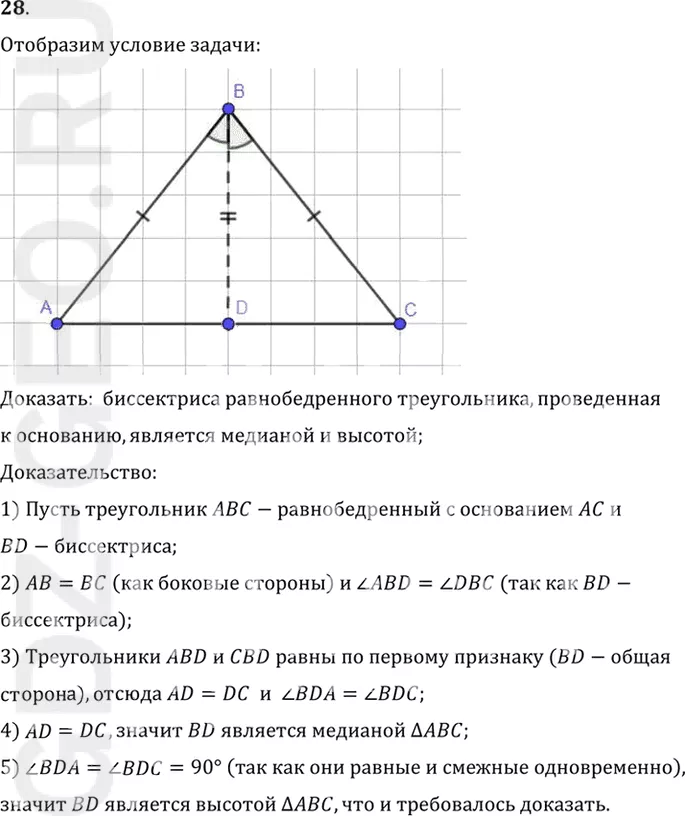
Доказать: биссектриса равнобедренного треугольника, проведенная

к основанию, является медианой и высотой;

Доказательство:

1) Пусть треугольник ABC-равнобедренный с основанием AC и

BD-биссектриса;

2) AB=BC (как боковые стороны) и угол ABD = углу DBC (так как BD-

биссектриса);

3) Треугольники ABD и CBD равны по первому признаку (BD-общая

сторона), отсюда AD=DC и угол BDA = углу BDC;

4) AD=DC, значит BD является медианой треугольник ABC;

5) угол BDA = углу BDC=90° (так как они равные и смежные одновременно),

значит BD является высотой треугольник ABC, что и требовалось доказать.

Развернуть