Условие:

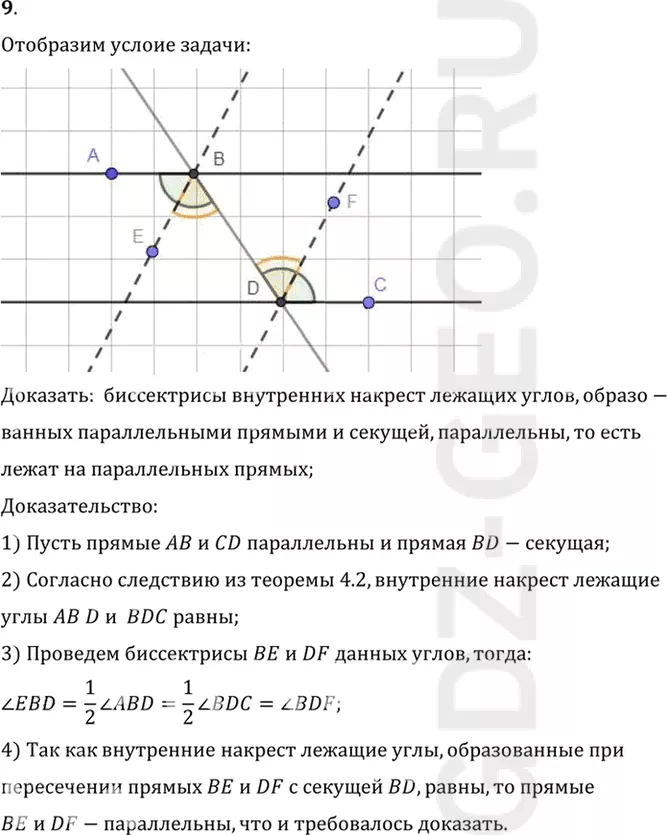
9. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных параллельными и секущей, параллельны, т. е. лежат на параллельных прямых.

Доказать: биссектрисы внутренних накрест лежащих углов, образо-

ванных параллельными прямыми и секущей, параллельны, то есть

лежат на параллельных прямых;

Доказательство:

1) Пусть прямые AB и CD параллельны и прямая BD-секущая;

2) Согласно следствию из теоремы 4.2, внутренние накрест лежащие

углы AB D и BDC равны;

3) Проведем биссектрисы BE и DF данных углов, тогда:

угол EBD=1/2 угол ABD=1/2 угол BDC = углу BDF;

4) Так как внутренние накрест лежащие углы, образованные при

пересечении прямых BE и DF с секущей BD, равны, то прямые

BE и DF-параллельны, что и требовалось доказать.

Развернуть