Условие:

1. Докажите, что любой луч, исходящий из центра окружности, пересекает окружность в одной точке.

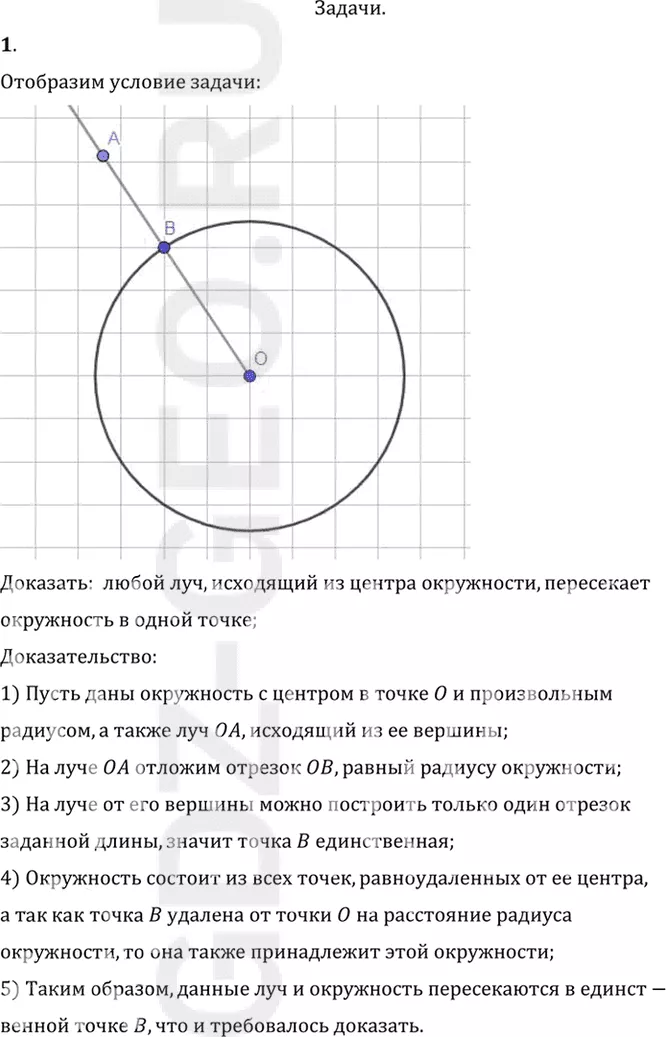
Доказать: любой луч, исходящий из центра окружности, пересекает

окружность в одной точке;

Доказательство:

1) Пусть даны окружность с центром в точке O и произвольным

радиусом, а также луч OA, исходящий из ее вершины;

2) На луче OA отложим отрезок OB, равный радиусу окружности;

3) На луче от его вершины можно построить только один отрезок

заданной длины, значит точка B единственная;

4) Окружность состоит из всех точек, равноудаленных от ее центра,

а так как точка B удалена от точки O на расстояние радиуса

окружности, то она также принадлежит этой окружности;

5) Таким образом, данные луч и окружность пересекаются в единст-

венной точке B, что и требовалось доказать.

Развернуть