Условие:

8. 1) Может ли окружность касаться прямой в двух точках? Объясните ответ.

2) Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания.

I)

Выяснить: может ли окружность касаться прямой в двух точках;

Решение:

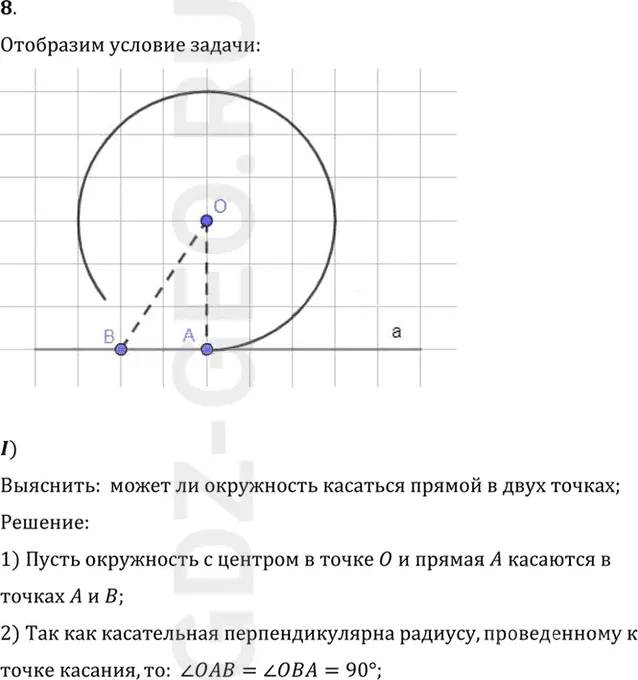
1) Пусть окружность с центром в точке O и прямая A касаются в

точках A и B;

2) Так как касательная перпендикулярна радиусу, проведенному к

точке касания, то: угол OAB = углу OBA=90°;

3) Таким образом, треугольник OAB имеет два прямых угла, что

невозможно, значит прямая и окружность могут иметь только

одну точку касания;

Ответ: не могут.

II)

Доказать: касательная к окружности не имеет с ней других общих

точек, кроме точки касания;

Доказательство:

1) Пусть a-касатеьная к окружности в точке A;

2) Допустим, касательная и окружность имеют, кроме точки A, общую

точку B, отличную от A;

3) Треугольник AOB равнобедренный с основанием AB (OA=OB=r),

значит у него углы A и B равны;

4) Так как касательная перпендикулярна радиусу, проведенному к

точке касания, то: угол OAB = углу OBA=90°, то есть у треугольник AOB два прямых

угла, что невозможно, значит касательная к окружности не имеет с ней

других общих точек, кроме точки касания, что и требовалось доказать.

Развернуть