Условие:

16. 1) Из одной точки проведены две касательные к окружности (рис. 108). Докажите, что отрезки касательных МР и MQ равны.

2) Докажите, что через одну точку не может проходить больше двух касательных к окружности.

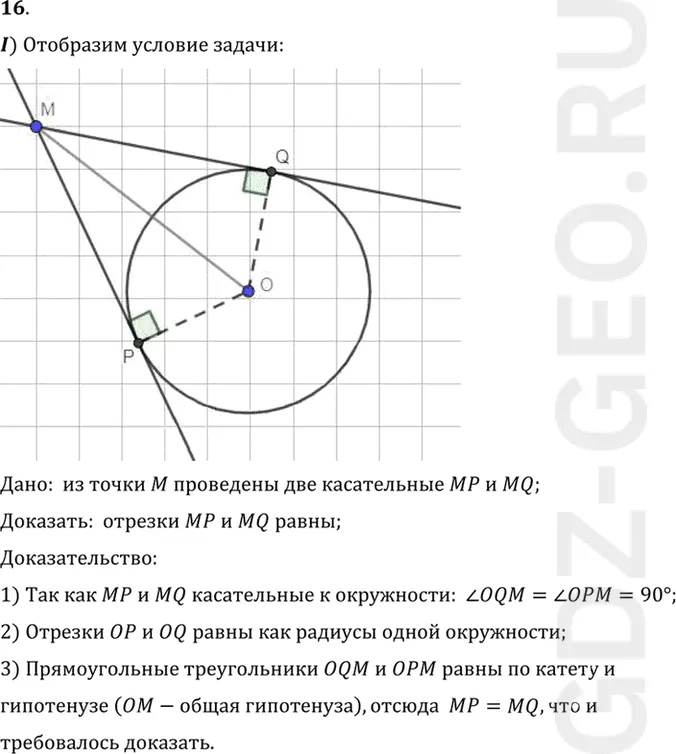
I) Отобразим условие задачи:

Дано: из точки M проведены две касательные MP и MQ;

Доказать: отрезки MP и MQ равны;

Доказательство:

1) Так как MP и MQ касательные к окружности: угол OQM = углу OPM=90°;

2) Отрезки OP и OQ равны как радиусы одной окружности;

3) Прямоугольные треугольники OQM и OPM равны по катету и

гипотенузе (OM-общая гипотенуза), отсюда MP=MQ, что и

требовалось доказать.

II)

Доказать: через одну точку не может проходить больше двух

касательных к окружности;

Доказательство:

1) Пусть даны окружность с центром в точке O1 и точка M, лежащая

вне этой окружности;

2) Допустим, что через точку M проходит три прямых, касающихся

окружности в точках A, B и C, тогда согласно пункту I этой задачи:

AM=BM=MC;

3) Значит точки A, B и C лежат на одной окружности с центром в

точке M, но две окружности не могут иметь более двух точек

пересечения (задача 14 пункт II), значит допущение неверно и через

одну точку можно провести не более двух касательных к окружности,

что и требовалось доказать.

Развернуть