Условие:

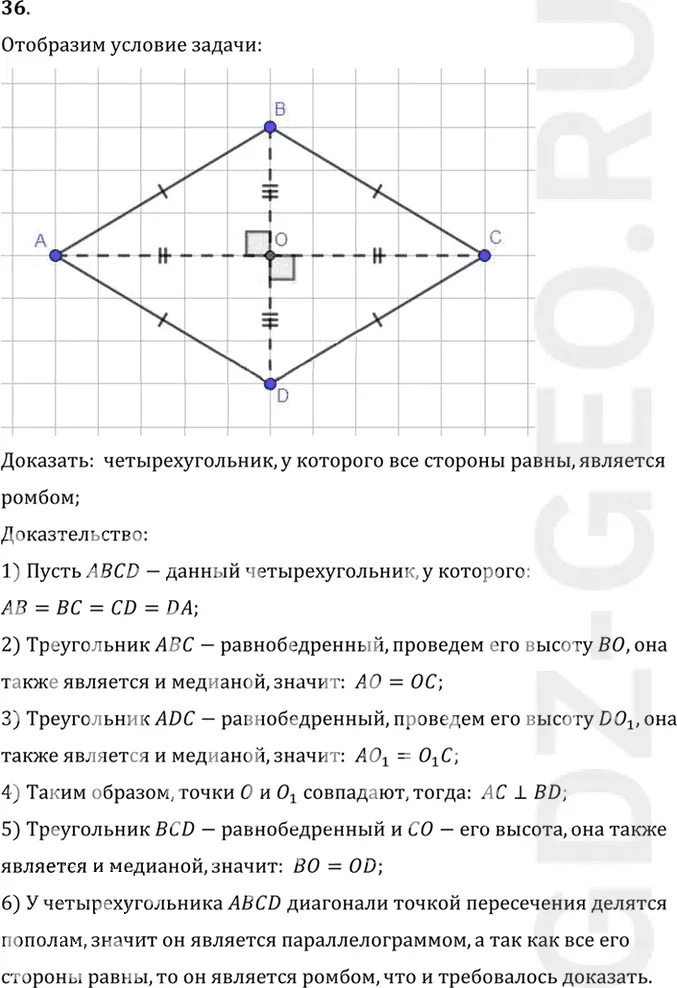
36. Докажите, что четырёхугольник, у которого все стороны равны, является ромбом.

Доказать: четырехугольник, у которого все стороны равны, является

ромбом;

Доказтельство:

1) Пусть ABCD-данный четырехугольник, у которого:

AB=BC=CD=DA;

2) Треугольник ABC-равнобедренный, проведем его высоту BO, она

также является и медианой, значит: AO=OC;

3) Треугольник ADC-равнобедренный, проведем его высоту DO1, она

также является и медианой, значит: AO1=O1 C;

4) Таким образом, точки O и O1 совпадают, тогда: AC перпендикулярен BD;

5) Треугольник BCD-равнобедренный и CO-его высота, она также

является и медианой, значит: BO=OD;

6) У четырехугольника ABCD диагонали точкой пересечения делятся

пополам, значит он является параллелограммом, а так как все его

стороны равны, то он является ромбом, что и требовалось доказать.

Развернуть