Условие:

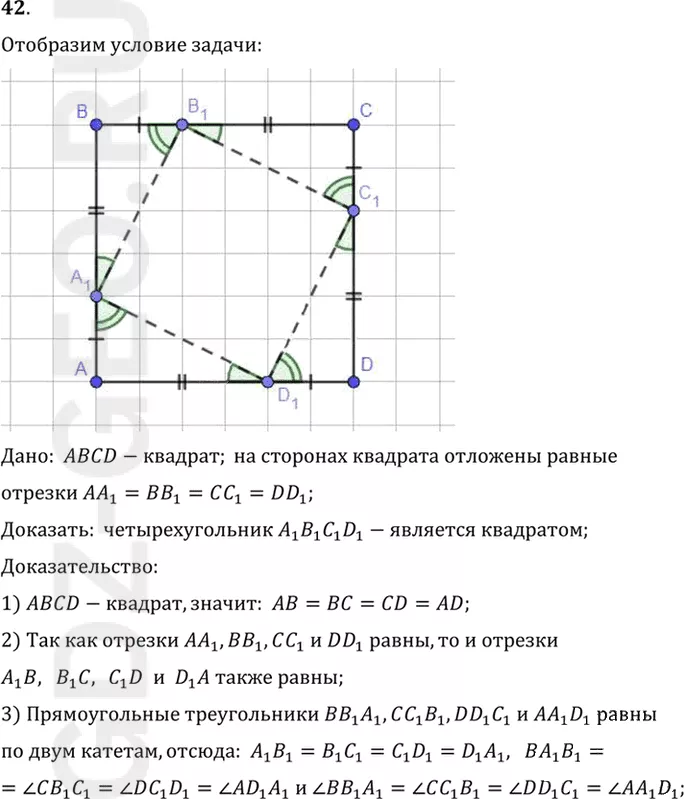
42. На каждой стороне квадрата AJBCD отложены равные отрезки: АА1 = ВВ1 = СС1 = DD1. Докажите, что четырёхугольник A1B1C1D1 есть квадрат (рис. 145).

Дано: ABCD-квадрат; на сторонах квадрата отложены равные

отрезки AA1=BB1=CC1=DD1;

Доказать: четырехугольник A1 B1 C1 D1-является квадратом;

Доказательство:

1) ABCD-квадрат, значит: AB=BC=CD=AD;

2) Так как отрезки AA1, BB1, CC1 и DD1 равны, то и отрезки

A1 B, B1 C, C1 D и D1 A также равны;

3) Прямоугольные треугольники BB1 A1, CC1 B1, DD1 C1 и AA1 D1 равны

по двум катетам, отсюда: A1 B1=B1 C1=C1 D1=D1 A1, BA1 B1=

= углу CB1 C1 = углу DC1 D1 = углу AD1 A1 и угол BB1 A1 = углу CC1 B1 = углу DD1 C1 = углу AA1 D1;

4) Так как все стороны четырехугольника A1 B1 C1 D1 равны, то он

является ромбом;

5) Треугольник BB1 A1-прямоугольный, следовательно:

угол BB1 A1+ угол BA1 B1=180°- угол A1 BB1=180°-90°=90°;

6) Докажем, что угол A1 B1 C1-прямой:

угол A1 B1 C1 = углу BB1 C-(угол BB1 A1+ угол C1 B1 C);

угол A1 B1 C1 = углу BB1 C-(угол BB1 A1+ угол BA1 B1)=180°-90°=90°;

7) Аналогично доказыается, что углы B1 C1 D1, C1 D1 A1 и D1 A1 B1 также

являются прямыми;

8) Так как у ромба A1 B1 C1 D1 все углы прямые, то он является квадратом,

что и требуется доказать.

Развернуть