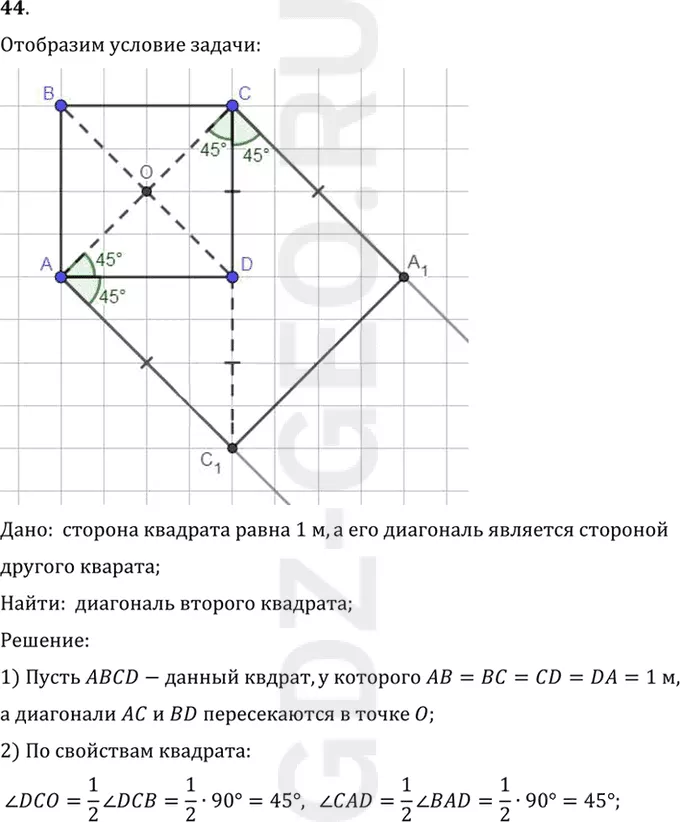
Условие:

44. Дан квадрат, сторона которого 1 м, диагональ его равна стороне другого квадрата. Найдите диагональ последнего.

Дано: сторона квадрата равна 1 м, а его диагональ является стороной

другого кварата;

Найти: диагональ второго квадрата;

Решение:

1) Пусть ABCD-данный квдрат, у которого AB=BC=CD=DA=1 м,

а диагонали AC и BD пересекаются в точке O;

2) По свойствам квадрата:

угол DCO=1/2 угол DCB=1/2•90°=45°, угол CAD=1/2 угол BAD=1/2•90°=45°;

3) На концах отрезка AC построим углы в 45°, отложим на них отрезки

AC1 и CA1, равные AC;

4) угол CAC1 = углу CAD+ угол DAC1=45°+45°=90°;

угол ACA1 = углу ACD+ угол DCA1=45°+45°=90°;

5) AC1 перпендикулярен AC и CA1 перпендикулярен AC, следовательно AC1 ||CA1;

6) Так как противолежащие стороны четырехугольника ACA1 C1 равны

и параллельны, то он является параллелограммом, отсюда A1 C1=AC;

7) Таким образом, все стороны в ACA1 C1 равны, следовательно он

является ромбом, а так как рядом лежащие углы равны 90°, то все его

углы-прямые, значит ACA1 C1-квадрат;

8) AC-сторона ACA1 C1, следовательно этот квадрат искомый, у него

CC1=CD+DC1=1+1=2 м (по свйству квадрата);

Ответ: 2 м.

Развернуть