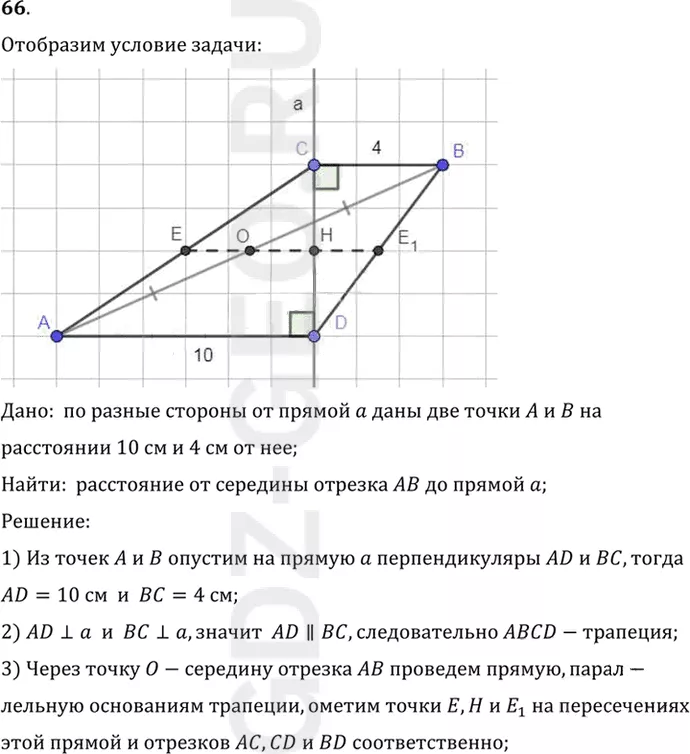
Условие:

66. По разные стороны от прямой а даны две точки А и В на расстояниях 10 см и 4 см от неё. Найдите расстояние от середины отрезка АВ до прямой а.

Дано: по разные стороны от прямой a даны две точки A и B на

расстоянии 10 см и 4 см от нее;

Найти: расстояние от середины отрезка AB до прямой a;

Решение:

1) Из точек A и B опустим на прямую a перпендикуляры AD и BC, тогда

AD=10 см и BC=4 см;

2) AD перпендикулярен a и BC перпендикулярен a, значит AD||BC, следовательно ABCD-трапеция;

3) Через точку O-середину отрезка AB проведем прямую, парал-

лельную основаниям трапеции, ометим точки E, H и E1 на пересечениях

этой прямой и отрезков AC, CD и BD соответственно;

4) AO=OB (по построению), тогда согласно теореме Фалеса:

AE=EC (для сторон угла CAB) и BE1=E1 D (для сторон угла ABD),

отсюда следует, что CH=HD (для сторон угла CDB);

5) В треугольнике ACD отрезок EH-средняя линия, значит:

EH=1/2 AD=1/2•10=5 см;

6) В треугольнике ACB отрезок EO-средняя линия, значит:

EO=1/2 BC=1/2•4=2 см;

7) AD перпендикулярен a и OH||AD, следовательно OH перпендикулярен a, отрезок OH-искомое

расстояне;

8) OH=EH-EO=5-2=3 см;

Ответ: 3 см.

Развернуть