Условие:

73. Даны отрезки а, b, с, d, е. Постройте отрезок х=abc/de.

Построение:

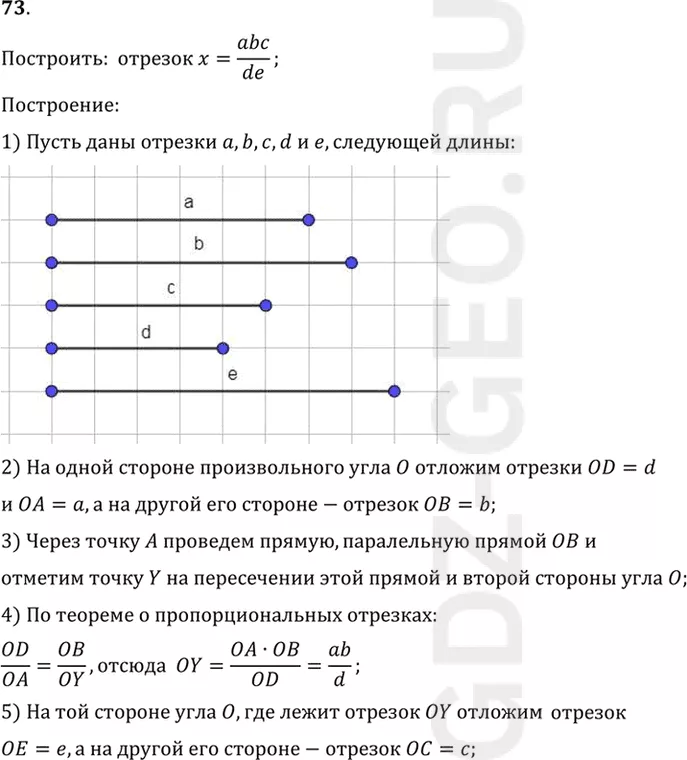
1) Пусть даны отрезки a, b, c, d и e, следующей длины.

2) На одной стороне произвольного угла O отложим отрезки OD=d

и OA=a, а на другой его стороне-отрезок OB=b;

3) Через точку A проведем прямую, паралельную прямой OB и

отметим точку Y на пересечении этой прямой и второй стороны угла O;

4) По теореме о пропорциональных отрезках:

OD/OA=OB/OY, отсюда OY=(OA•OB)/OD=ab/d;

5) На той стороне угла O, где лежит отрезок OY отложим отрезок

OE=e, а на другой его стороне-отрезок OC=c;

6) Через точку Y проведем прямую, паралельную прямой EC и

отметим точку X на пересечени этой прямой и второй стороны угла O;

7) По теореме о пропорциональных отрезках:

OE/OY=OC/OX, отсюда OX=(OY•OC)/OE=abc/de;

8) Отрезок OX-искомый

Развернуть