Условие:

20. Докажите теорему о пропорциональных отрезках.

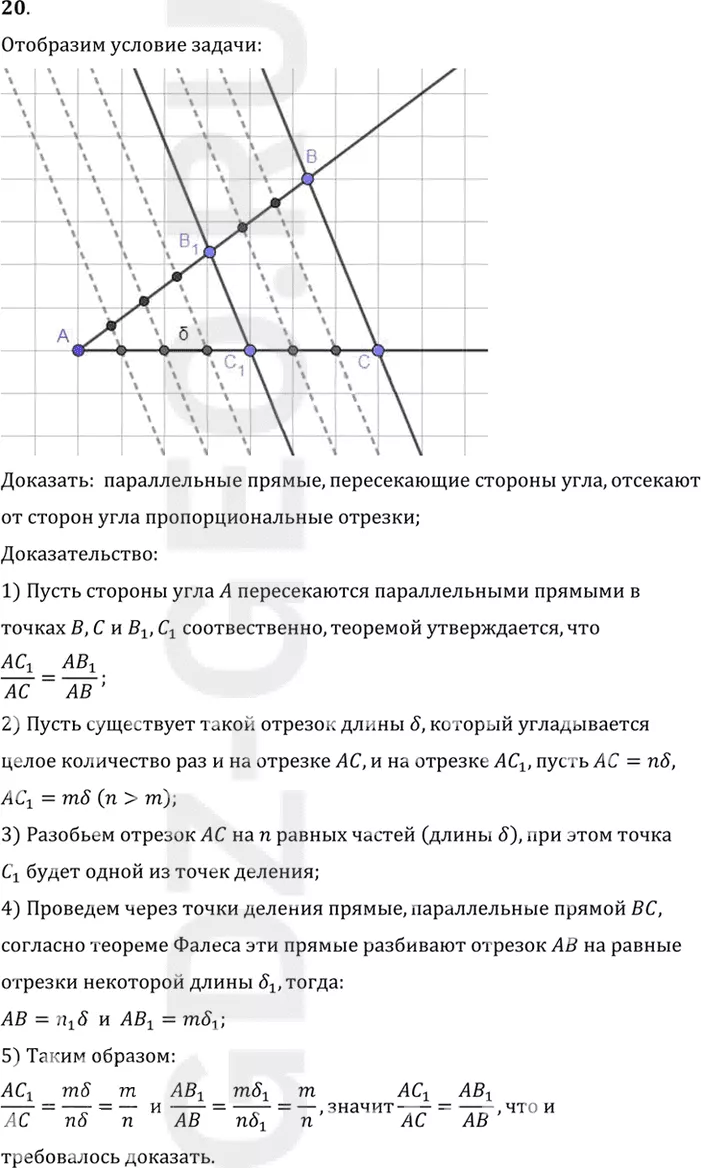
Отобразим условие задачи:

Доказать: параллельные прямые, пересекающие стороны угла, отсекают

от сторон угла пропорциональные отрезки;

Доказательство:

1) Пусть стороны угла A пересекаются параллельными прямыми в

точках B, C и B1, C1 соотвественно, теоремой утверждается, что

(AC1)/AC=(AB1)/AB;

2) Пусть существует такой отрезок длины ?, который угладывается

целое количество раз и на отрезке AC, и на отрезке AC1, пусть AC=n?,

AC1=m? (n>m);

3) Разобьем отрезок AC на n равных частей (длины ?), при этом точка

C1 будет одной из точек деления;

4) Проведем через точки деления прямые, параллельные прямой BC,

согласно теореме Фалеса эти прямые разбивают отрезок AB на равные

отрезки некоторой длины ?1, тогда:

AB=n1 ? и AB1=m?1;

5) Таким образом:

(AC1)/AC=m?/n?=m/n и (AB1)/AB=(m?1)/(n?1)=m/n, значит (AC1)/AC=(AB1)/AB, что и

требовалось доказать.

Развернуть