Условие:

24. Даны три попарно пересекающиеся прямые а, b, с. Как построить отрезок, перпендикулярный прямой b, с серединой на прямой b и концами на прямых а и с (рис. 212)? Всегда ли задача имеет решение?

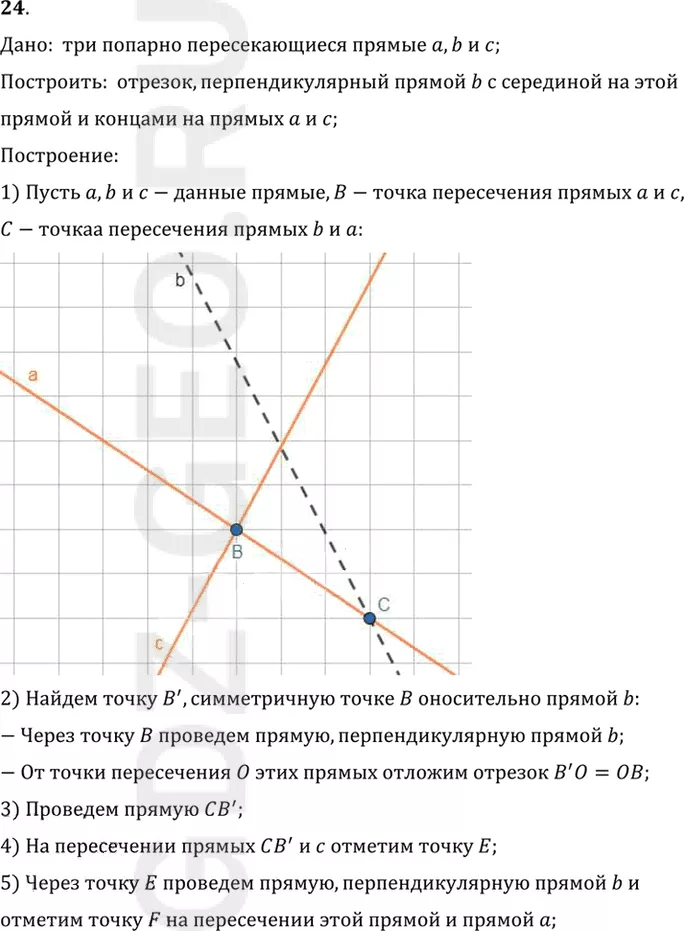
Дано: три попарно пересекающиеся прямые a, b и c;

Построить: отрезок, перпендикулярный прямой b с серединой на этой

прямой и концами на прямых a и c;

Построение:

1) Пусть a, b и c-данные прямые, B-точка пересечения прямых a и c,

C-точкаа пересечения прямых b и a.

2) Найдем точку B', симметричную точке B оносительно прямой b:

- Через точку B проведем прямую, перпендикулярную прямой b;

- От точки пересечения O этих прямых отложим отрезок B' O=OB;

3) Проведем прямую CB';

4) На пересечении прямых CB' и c отметим точку E;

5) Через точку E проведем прямую, перпендикулярную прямой b и

отметим точку F на пересечении этой прямой и прямой a;

6) Прямая b является осью симметрии и биссектрисой угла BCB',

значит она является медианой и высотой треугольника ECF, у

которого вершины E и F лежат на сторонах угла BCB';

7) Значит отрезок EF-искомый