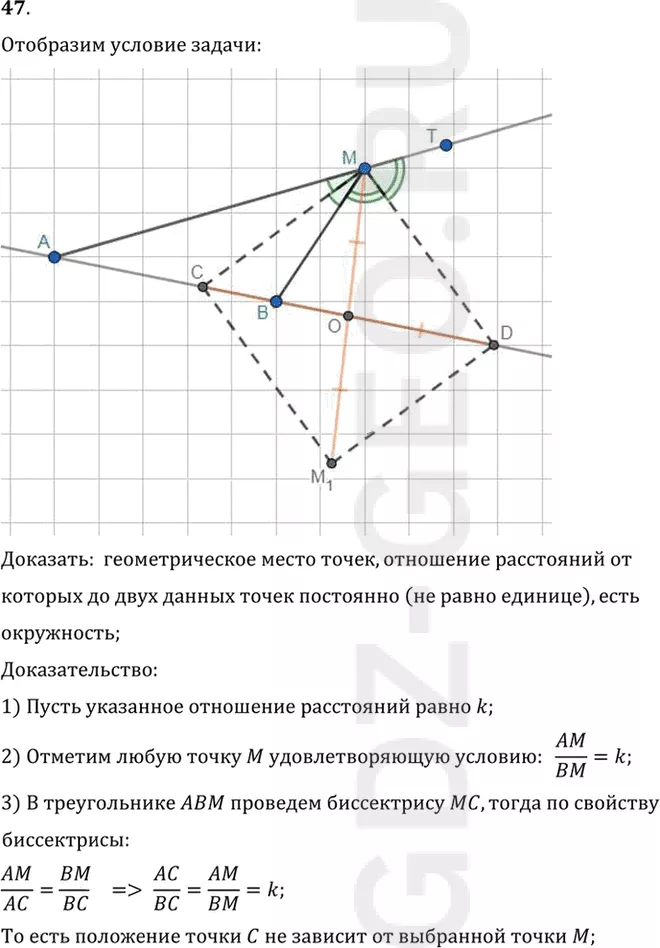
Условие:

47 Докажите, что геометрическое место точек, отношение расстояний от которых до двух данных точек постоянно (не равно единице), есть окружность.

Доказать: геометрическое место точек, отношение расстояний от

которых до двух данных точек постоянно (не равно единице), есть

окружность;

Доказательство:

1) Пусть указанное отношение расстояний равно k;

2) Отметим любую точку M удовлетворяющую условию: AM/BM=k;

3) В треугольнике ABM проведем биссектрису MC, тогда по свойству

биссектрисы:

AM/AC=BM/BC => AC/BC=AM/BM=k;

То есть положение точки C не зависит от выбранной точки M;

4) Построим биссектрису внешнего угла при вершине M треугольник ABM, она

пересечет прямую AB в точке D, тогда по доказанному в задаче 11.46:

AD/BD=AM/BM=k;

То есть положение точки D также не зависит от выбранной точки M;

5) Прямые MC и MD-биссектрисы внешнего и внутреннего углов:

2угол CMB+2угол BMD = углу AMT;

2(угол CMB+ угол BMD)=180°;

2угол CMD=180°, отсюда угол CMD=90°;

6) Отметим точку O-середину отрезка CD;

7) Достроим прямоугольный треугольник CMD до прямоугольника CMDM1, тогда

O-точка пересечения диагоналей: MO=CO=OD=OM1=1/2 CD;

8) Отрезок CD не зависит от выбора точки M, значит все точки,

удовлетворяющие условию, будут равноудалены от точки O, значит

множество этих точек является окружностью (по определению), что и

требовалось доказать.

Развернуть