Условие:

8. Сформулируйте и докажите признак подобия треугольников по двум сторонам и углу между ними.

I) Признак подобия треугольников по двум сторонам и углу между ними:

Если две стороны одного треугольника пропорциональны двум сторонам

другого треугольника и углы, образованные этими сторонами, равны,

то треугольники подобны;

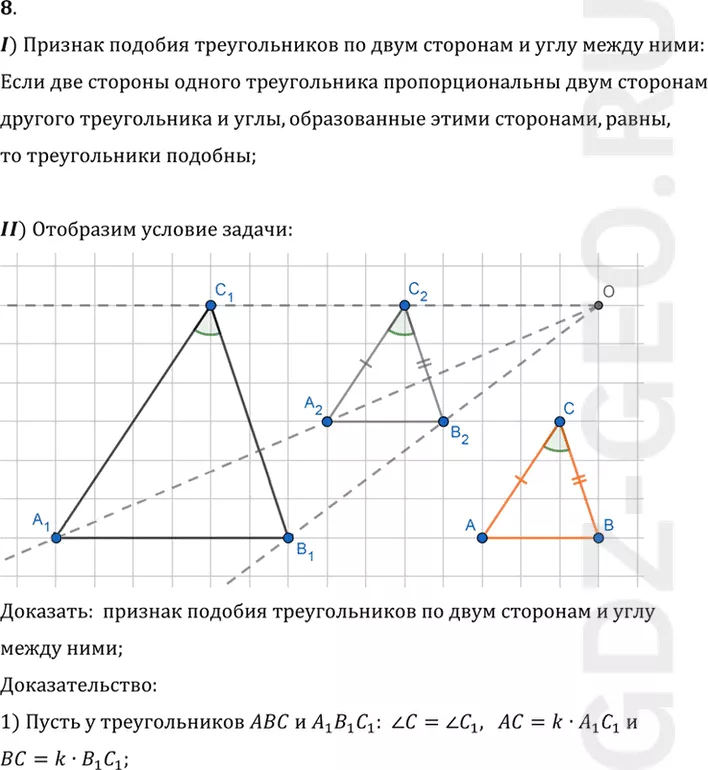
II) Отобразим условие задачи:

Доказать: признак подобия треугольников по двум сторонам и углу

между ними;

Доказательство:

1) Пусть у треугольников ABC и A1 B1 C1: угол C = углу C1, AC=k•A1 C1 и

BC=k•B1 C1;

2) Подвергнем треугольник A1 B1 C1 преобразованию подобия с

коэффициентом подобия k, например гомотетии, при этом получим

некоторый треугольник A2 B2 C2;

3) Рассмотрим треугольники ABC и A2 B2 C2:

угол C2 = углу C1 = углу C (так как преобразование подобия сохраняет углы),

A2 C2=k•A1 C1=AC и B2 C2=k•B1 C1=BC, следовательно эти

треугольники равны по первому признаку;

4) Так как треугольники A1 B1 C1 и A2 B2 C2 гомотетичны и подобны, а

треугольники A2 B2 C2 и ABC равны и поэтому тоже подобны, то

треугольники A1 B1 C1 и ABC подобны, что и требовалось доказать.

Развернуть