Условие:

17. Докажите, что угол, вершина которого лежит внутри окружности, равен полусумме двух центральных углов, которым соответствуют дуги окружности, заключённые между сторонами данного угла и их продолжениями.

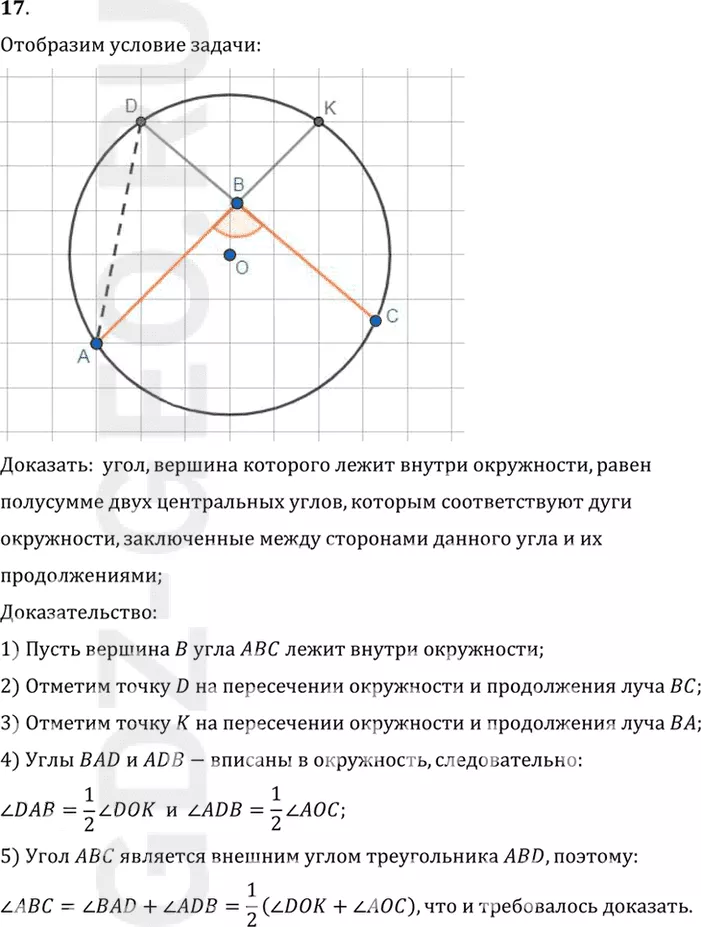
Доказать: угол, вершина которого лежит внутри окружности, равен

полусумме двух центральных углов, которым соответствуют дуги

окружности, заключенные между сторонами данного угла и их

продолжениями;

Доказательство:

1) Пусть вершина B угла ABC лежит внутри окружности;

2) Отметим точку D на пересечении окружности и продолжения луча BC;

3) Отметим точку K на пересечении окружности и продолжения луча BA;

4) Углы BAD и ADB-вписаны в окружность, следовательно:

угол DAB=1/2 угол DOK и угол ADB=1/2 угол AOC;

5) Угол ABC является внешним углом треугольника ABD, поэтому:

угол ABC = углу BAD+ угол ADB=1/2 (угол DOK+ угол AOC), что и требовалось доказать.