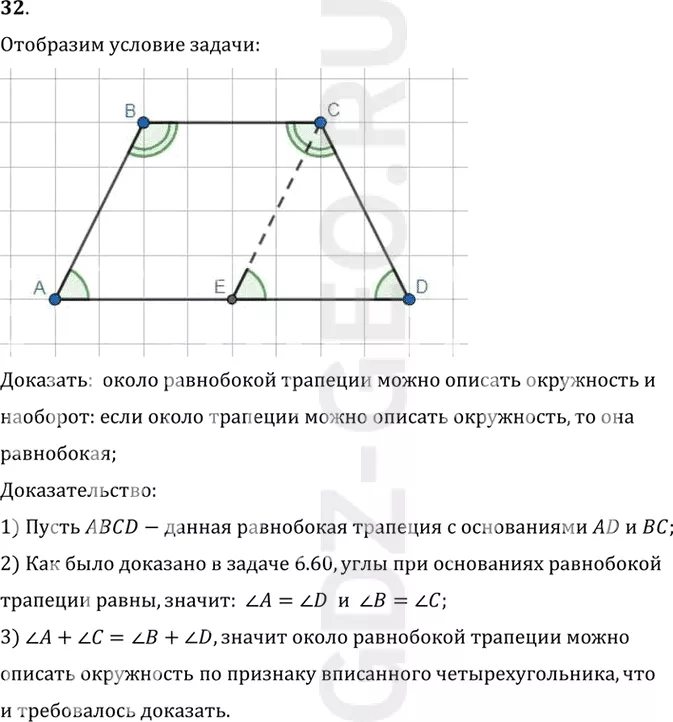
Условие:

32. Докажите, что около равнобокой трапеции можно описать окружность. Верно ли обратное утверждение?

Доказать: около равнобокой трапеции можно описать окружность и

наоборот: если около трапеции можно описать окружность, то она

равнобокая;

Доказательство:

1) Пусть ABCD-данная равнобокая трапеция с основаниями AD и BC;

2) Как было доказано в задаче 6.60, углы при основаниях равнобокой

трапеции равны, значит: угол A = углу D и угол B = углу C;

3) угол A+ угол C = углу B+ угол D, значит около равнобокой трапеции можно

описать окружность по признаку вписанного четырехугольника, что

и требовалось доказать.

4) Обратно: пусть около трапеции ABCD с основаниями AD и BC можно

описать окружность, тогда по свойству вписанного четырехугольника:

угол A+ угол C = углу B+ угол D=180°;

5) Рассмотрим параллельные прямые AD и BC и секущую CD:

угол C+ угол D=180° (как внутренние односторонние углы);

6) угол A+ угол C = углу C+ угол D=180°, отсюда угол A = углу D;

7) Через точку C проведем прямую, параллельную прямой AB и

пересекающую основание AD в точке E;

8) Четырехугольник ABCE-параллелограмм, значит: AB=CE;

9) Рассмотрим параллельные прямые AB и CE и секущую AE:

угол A = углу CED (как соответственные углы), тогда угол D = углу A = углу CED;

10) Треугольник ACD-равнобедренный с основанием ED, отсюда:

CE=CD, тогда AB=CE=CD, значит трапеция ABCD-равнобокая,

что и требовалось доказать.

Развернуть