Условие:

13. Сформулируйте и докажите свойство и признак вписанного четырёхугольника.

I) Свойство и признак вписанного четырехугольника:

У четырехугольника, вписанного в окружность, сумма противолежащих

углов равна 180°; и наоборот: если у четырехугольника сумма проти-

волежащих углов равна 180°, то около него можно описать окружность;

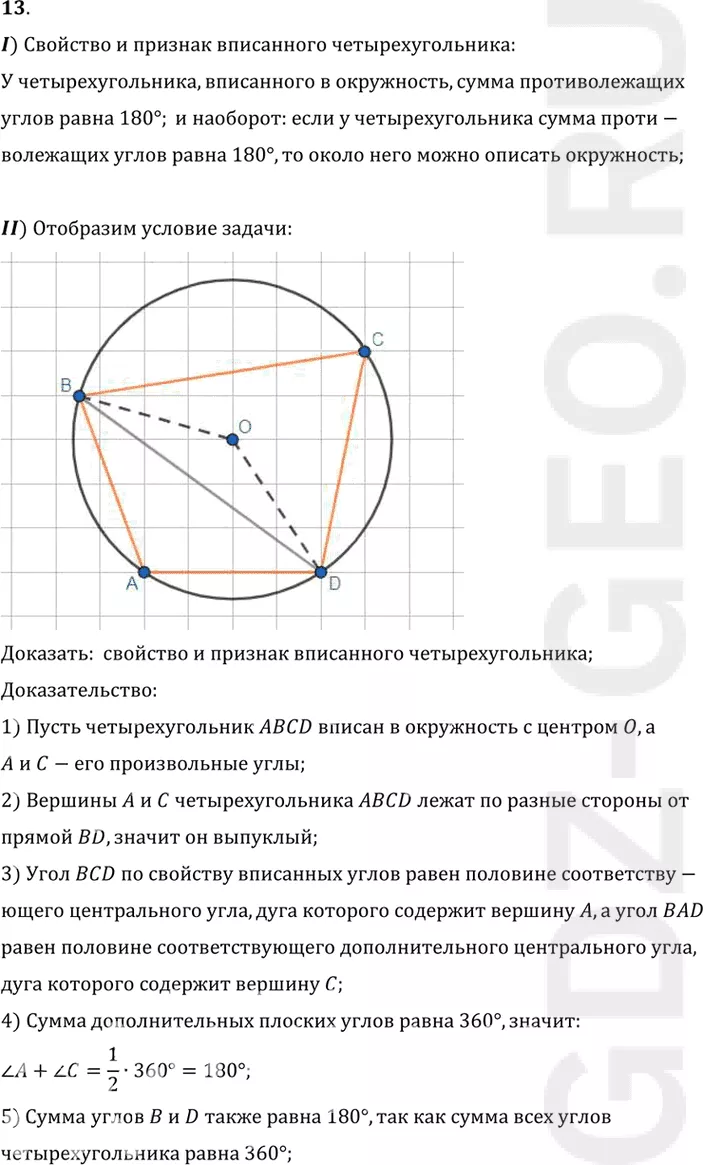
II) Отобразим условие задачи:

Доказать: свойство и признак вписанного четырехугольника;

Доказательство:

1) Пусть четырехугольник ABCD вписан в окружность с центром O, а

A и C-его произвольные углы;

2) Вершины A и C четырехугольника ABCD лежат по разные стороны от

прямой BD, значит он выпуклый;

3) Угол BCD по свойству вписанных углов равен половине соответству-

ющего центрального угла, дуга которого содержит вершину A, а угол BAD

равен половине соответствующего дополнительного центрального угла,

дуга которого содержит вершину C;

4) Сумма дополнительных плоских углов равна 360°, значит:

угол A + угол C=1/2•360°=180°;

5) Сумма углов B и D также равна 180°, так как сумма всех углов

четырехугольника равна 360°;

6) Таким образом угол A+ угол C = углу B+ угол D=180° , следовательно свойство

вписанного четырехугольника доказано.

7) Обратно: пусть у данного выпуклого четырехугольника ABCD сумма

противолежащих углов A и C равна 180°;

8) Опишем вокруг треугольника ABD окружность;

9) Вершины A и C лежат по разные стороны от прямой BD, потому что

по условию теоремы он выпуклый;

10) По доказанному градусная мера любого вписанного угла, стороны

которого проходят через точки B и D, а вершины лежат на дуге

построенной окружности, не содержащей вершины A, равна 180°-?A,

а значит, равна градусной мере угла C данного четырехугольника;

11) Следовательно, точка C как вершина угла, стороны которого

проходят через данные точки B и D, принадлежит геометрическому

месту вершин таких углов с той же градусной мерой и поэтому лежит

на окружности, описанной около треугольника ABD, значит признак

вписанного четырехугольника доказан.

Развернуть