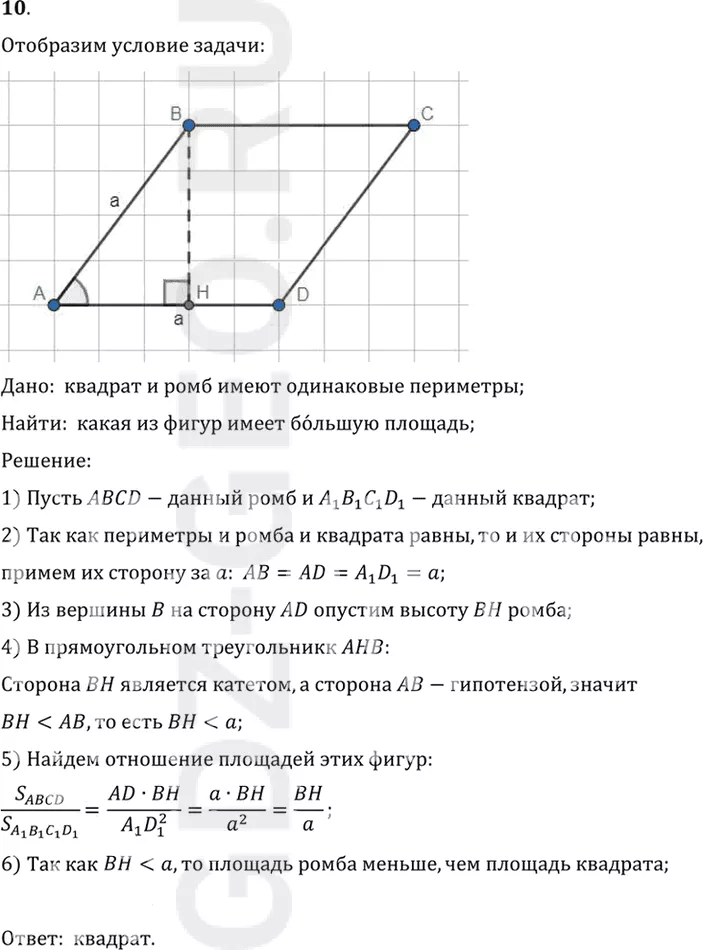
Условие:

10. Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? Объясните ответ.

Дано: квадрат и ромб имеют одинаковые периметры;

Найти: какая из фигур имеет большую площадь;

Решение:

1) Пусть ABCD-данный ромб и A1 B1 C1 D1-данный квадрат;

2) Так как периметры и ромба и квадрата равны, то и их стороны равны,

примем их сторону за a: AB=AD=A1 D1=a;

3) Из вершины B на сторону AD опустим высоту BH ромба;

4) В прямоугольном треугольникк AHB:

Сторона BH является катетом, а сторона AB-гипотензой, значит

BH < AB, то есть BH < a;

5) Найдем отношение площадей этих фигур:

SABCD/S(A1 B1 C1 D1 ) =(AD•BH)/(A1 D1^2 )=(a•BH)/a^2 =BH/a;

6) Так как BH < a, то площадь ромба меньше, чем площадь квадрата;

Ответ: квадрат.

Развернуть