Условие:

36 1) Докажите, что диагонали параллелограмма разбивают его на четыре равновеликих треугольника.

2) Диагонали трапеции ABCD с основаниями ВС и AD пересекаются в точке О. Докажите, что треугольники АВО и CDO равновеликие.

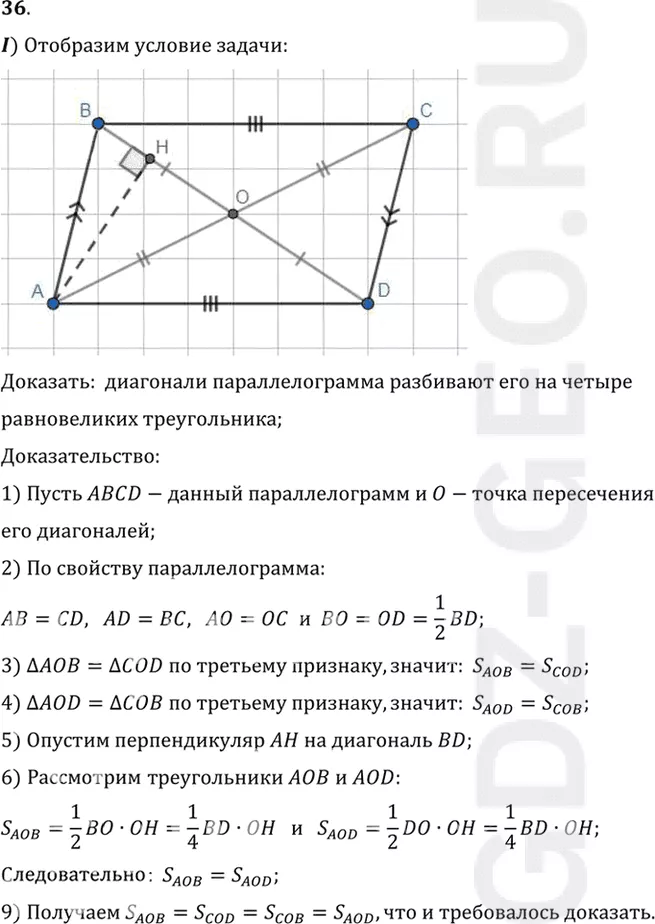
Доказать: диагонали параллелограмма разбивают его на четыре

равновеликих треугольника;

Доказательство:

1) Пусть ABCD-данный параллелограмм и O-точка пересечения

его диагоналей;

2) По свойству параллелограмма:

AB=CD, AD=BC, AO=OC и BO=OD=1/2 BD;

3) треугольник AOB = треугольник COD по третьему признаку, значит: SAOB=SCOD;

4) треугольник AOD = треугольник COB по третьему признаку, значит: SAOD=SCOB;

5) Опустим перпендикуляр AH на диагональ BD;

6) Рассмотрим треугольники AOB и AOD:

SAOB=1/2 BO•OH=1/4 BD•OH и SAOD=1/2 DO•OH=1/4 BD•OH;

Следовательно: SAOB=SAOD;

9) Получаем SAOB=SCOD=SCOB=SAOD, что и требовалось доказать.

II) Отобразим условие задачи:

Дано: диагонали трапеции ABCD с основаниями BC и AD пересекаются

в точке O;

Доказать: треугольники AOB и COD равновеликие;

Доказательство:

1) Из вершин B и C трапеции опустим высоты BB1 и CC1 на сторону AD,

они равны как расстояния между параллельными прямыми BC и AD:

BB1=CC1=h;

2) Рассмотрим треугольники ABD и DCA:

SABD=1/2 AD•BB1=1/2 AD•h и SDCA=1/2 AD•CC1=1/2 AD•h;

Следовательно: SABD=SDCA;

3) Треугольник ABD состоит из треугольника ABO и треугольника AOD, а треугольник DCA

состоит из треугольника COD и треугольника AOD, значит:

SABD=SAOB+SAOD и SACD=SCOD+SAOD;

Отсюда следует, что SAOB=SCOD, что и требовалось доказать.

Развернуть