Условие:

16. Расстояния от точки А до вершин квадрата равны а. Найдите расстояние от точки А до плоскости квадрата, если сторона квадрата равна b.

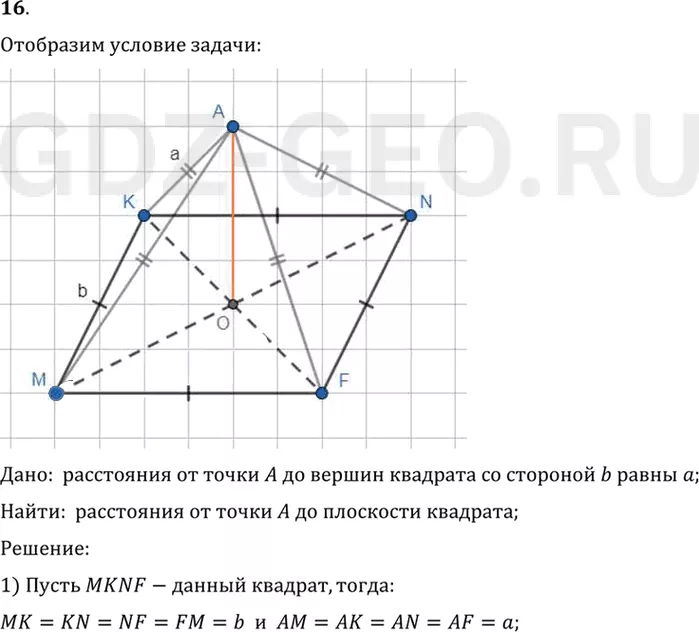
Дано: расстояния от точки A до вершин квадрата со стороной b равны a;

Найти: расстояния от точки A до плоскости квадрата;

Решение:

1) Пусть MKNF-данный квадрат, тогда:

MK=KN=NF=FM=b и AM=AK=AN=AF=a;

2) Опустим из точки A перендикуляр AO на плоскость квадрата MKNF;

3) Прямоугольные треугольники AOM, AOK, AON, AOF равны по

гипотенузе и общему катету AO, отсюда следует равенство их вторых

катетов: MO=KO=NO=FO;

4) Таким образом, точка O равноудалена от вершин квадрата MKNF,

значит она является центром описанной около него окружности, найдем

ее радиус:

MO=R=b/(2•sin(180°)/4)=b/(2•sin40°)=b/2•2/v2=b/v2;

5) В прямоугольном треугольнике AOM по теореме Пифагора:

AO=v(AM^2-MO^2 )=v(a^2-b^2/2);

Ответ: v(a^2-b^2/2).

Развернуть