Условие:

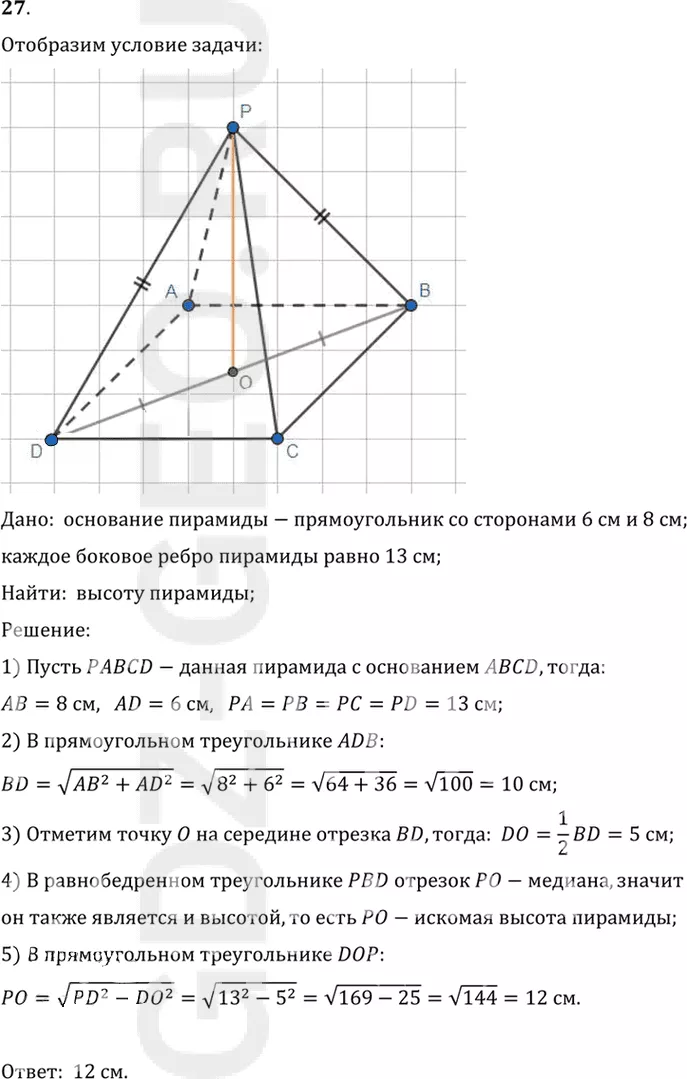
27. Основание пирамиды — прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.

Дано: основание пирамиды-прямоугольник со сторонами 6 см и 8 см;

каждое боковое ребро пирамиды равно 13 см;

Найти: высоту пирамиды;

Решение:

1) Пусть PABCD-данная пирамида с основанием ABCD, тогда:

AB=8 см, AD=6 см, PA=PB=PC=PD=13 см;

2) В прямоугольном треугольнике ADB:

BD=v(AB^2+AD^2 )=v(8^2+6^2 )=v(64+36)=v100=10 см;

3) Отметим точку O на середине отрезка BD, тогда: DO=1/2 BD=5 см;

4) В равнобедренном треугольнике PBD отрезок PO-медиана, значит

он также является и высотой, то есть PO-искомая высота пирамиды;

5) В прямоугольном треугольнике DOP:

PO=v(PD^2-DO^2)=v(13^2-5^2 )=v(169-25)=v144=12 см.

Ответ: 12 см.

Развернуть