Условие:

28. Основание пирамиды — параллелограмм, у которого стороны 3 см и 7 см, а одна из диагоналей 6 см; высота пирамиды проходит через точку пересечения диагоналей, она равна 4 см. Найдите боковое ребро пирамиды.

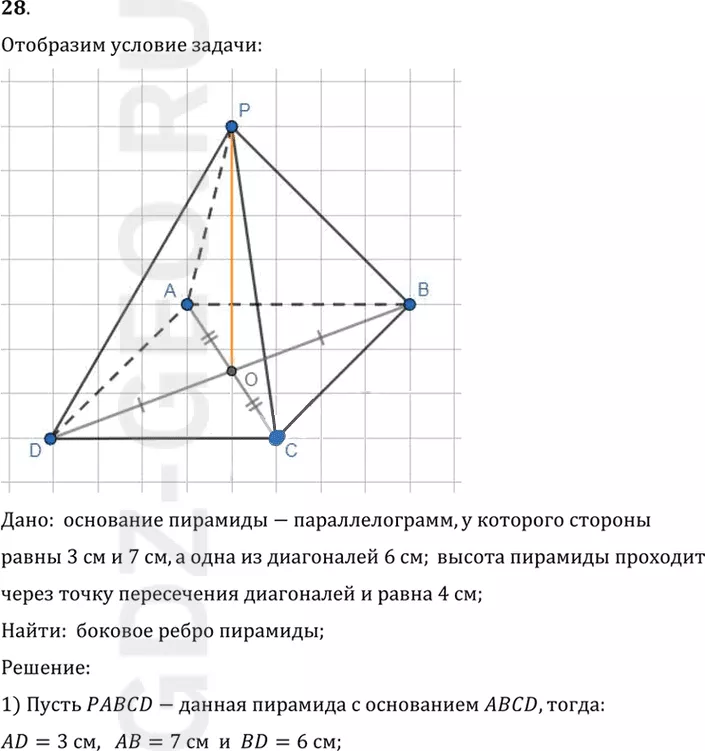
Дано: основание пирамиды-параллелограмм, у которого стороны

равны 3 см и 7 см, а одна из диагоналей 6 см; высота пирамиды проходит

через точку пересечения диагоналей и равна 4 см;

Найти: боковое ребро пирамиды;

Решение:

1) Пусть PABCD-данная пирамида с основанием ABCD, тогда:

AD=3 см, AB=7 см и BD=6 см;

2) По доказанному в задаче 10.38 сумма квадратов диагоналей парал-

лелограмма равна сумме квадратов всех его сторон:

2(AB^2+AD^2 )=AC^2+BD^2,отсюда AC^2=2(AB^2+AD^2 )-BD^2;

AC^2=2•(7^2+3^2)-6^2=2•(49+9)-36=2•58-36=80;

AC=v80=v(16•5)=4v5 см;

3) Проведем высоту PO пирамиды, тогда по условию задачи:

PO=4 см и точка O лежит на пересечении диагоналей AC и BD;

DO=1/2 BD=3 см и AO=1/2 AC=2v5 см;

4) В прямоугольном треугольнике DOP:

DP=v(DO^2+PO^2 )=v(3^2+4^2 )=v(9+16)=v25=5 см;

5) В прямоугольном треугольнике AOP:

AP=v(AO^2+PO^2 )=v((2v5)^2+4^2 )=v(4•5+16)=v36=6 см.

Ответ: 5 см и 6 см.