Условие:

44. Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объём пирамиды?

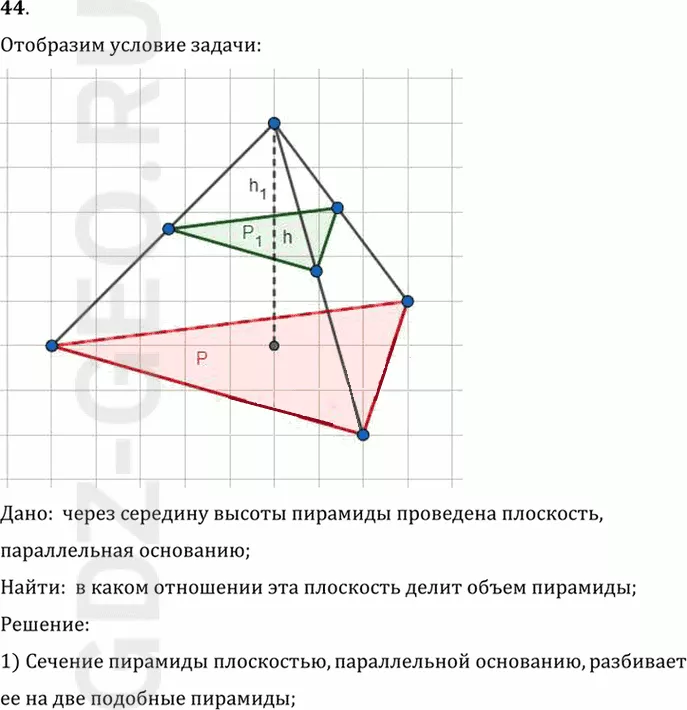
Дано: через середину высоты пирамиды проведена плоскость,

параллельная основанию;

Найти: в каком отношении эта плоскость делит объем пирамиды;

Решение:

1) Сечение пирамиды плоскостью, параллельной основанию, разбивает

ее на две подобные пирамиды;

2) Пусть многоугольники P и P1-основания полной и отсекаемой

пирамиды соответственно, h-высота полной пирамиды и h1-высота

пирамиды, образованной сечением, тогда:

h1=h/2;

3) Примем коэффициент подобия пирамид за число k, тогда:

k=h/h2 =h:h/2=h•2/h=2;

4) Объемы подобных тел относятся как кубы их соответствующих

ленейных размеров, значит:

V/V1 =k^3=2^3=8,отсюда V1=1/8 V;

5) Таким образом, плоскость отсекает от полной пирамиды:

пирамиду объемом 1/8 V и усеченную приамиду объемом 7/8 V, значит

отношение этих частей равно 1:7.

Ответ: 1:7.

Развернуть