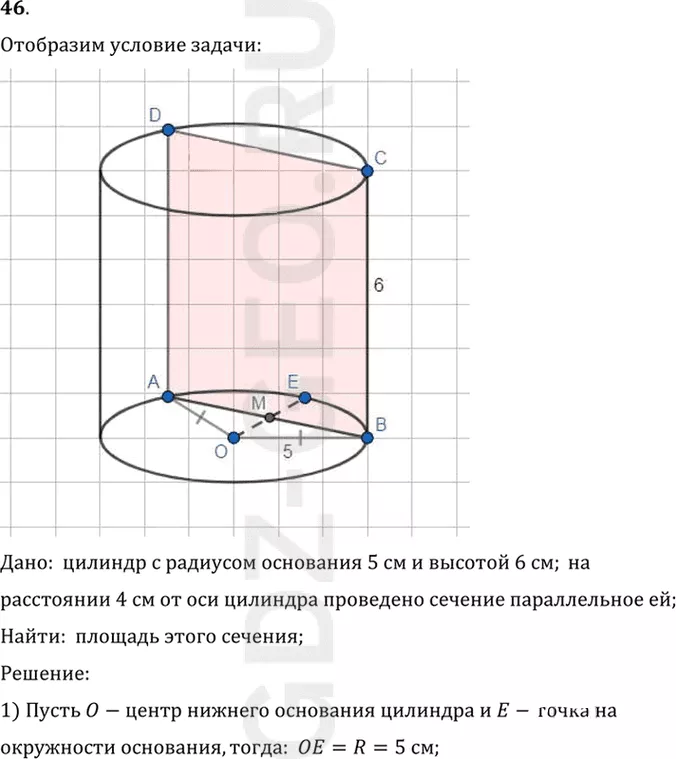
Условие:

46. Высота цилиндра 6 см, радиус основания 5 см. Найдите площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4 см от неё.

Дано: цилиндр с радиусом основания 5 см и высотой 6 см; на

расстоянии 4 см от оси цилиндра проведено сечение параллельное ей;

Найти: площадь этого сечения;

Решение:

1) Пусть O-центр нижнего основания цилиндра и E-точка на

окружности основания, тогда: OE=R=5 см;

2) Рассмотрим искомое сечение ABCD, оно является прямоугольником,

так как параллельно оси цилиндра;

3) Отметим точку M на пересечении отрезков AB и OE, тогда:

OA=OB=R=5 см, OM перпендикулярен AB и OM=4 см;

4) В прямоугольном треугольнике AOM по теореме Пифагора:

AM=v(OA^2-OM^2 )=v(5^2-4^2 )=v(25-16)=v9=3 см;

5) Треугольник AOB-равнобедренный, значит его высота OM является

и медианой, тогда: AB=2AM=6 см;

6) Отрезки AD и CB являются образующими цилиндра, значит они

равны его высоте: AD=CB=h=6 см;

7) Найдем площадь прямоугольника ABCD:

S=AB•AD=6•6=36 см^2;

Ответ: 36 см^2;

Развернуть