Условие:

52. Радиусы оснований усечённого конуса 3 дм и 7 дм, образующая 5 дм. Найдите площадь осевого сечения.

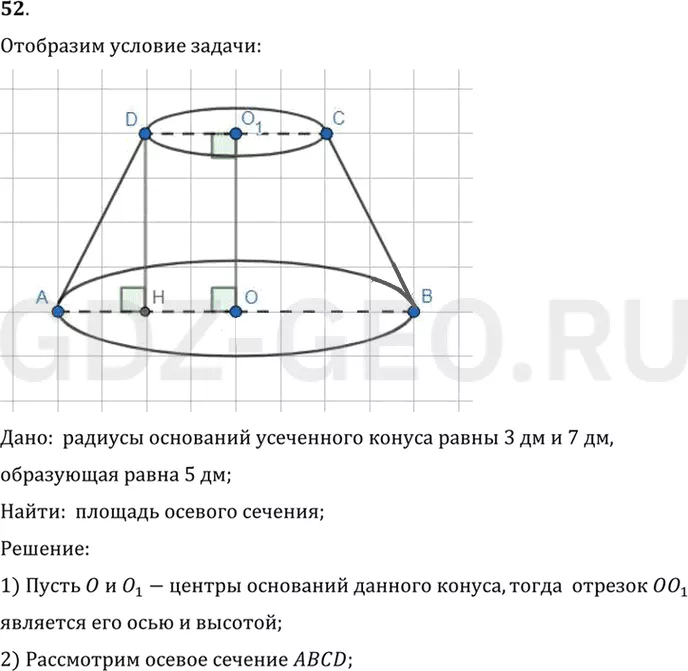
Дано: радиусы оснований усеченного конуса равны 3 дм и 7 дм,

образующая равна 5 дм;

Найти: площадь осевого сечения;

Решение:

1) Пусть O и O1-центры оснований данного конуса, тогда отрезок OO1

является его осью и высотой;

2) Рассмотрим осевое сечение ABCD;

3) Отрезки AB и CD параллельны, так как они лежат в параллельных

плоскостях, а также они являются диаметрами оснований, значит

четырехугольник ABCD-трапеция, у которой:

OA=OB=7 дм, AB=2•OA=14 дм, O1 C=O1 D=3 дм и

CD=2•O1 C=6 дм;

4) Отрезки AD и CB являются образующими конуса, значит:

AD=CB=5 дм;

5) Из точки D опустим перпендикуляр DH на отрезок OA;

6) OO1 перпендикулярен O1 D, OO1?OA и DH перпендикулярен OA, значит четырехугольник OHDO1

является прямоугольником, отсюда: DH=OO1 и OH=O1 D=3 дм;

7) AH=OA-OH=7-3=4 дм;

8) В прямоугольном треугольнике AHD по теореме Пифагора:

DH=v(AD^2-AH^2 )=v(5^2-4^2 )=v(25-16)=v9=3 дм;

9) Найдем площадь трапеции ABCD:

S=(AB+CD)/2•DH=(14+6)/2•3=10•3=30 дм^2.

Ответ: 30 дм^2.

Развернуть